MMCS (Mixed Matrix Commitment Scheme)
Merkle Tree 用于对向量(单列数据)承诺,而 MMCS (Mixed Matrix Commitment Scheme) 支持对多个不同高度和宽度的矩阵进行承诺和验证。
构造 MMCS
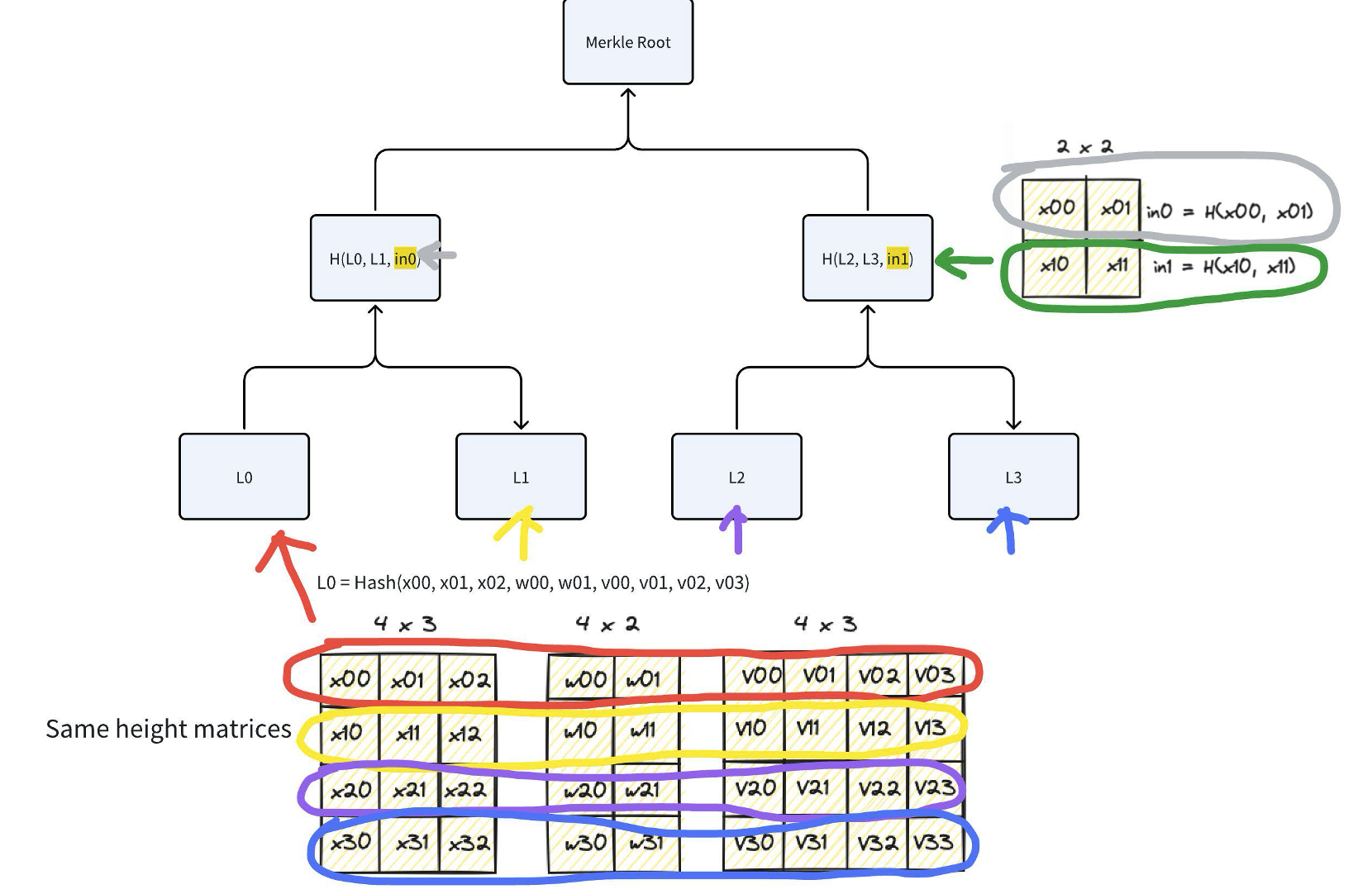
图片来源:merkle-tree.ipynb
如图所示,共有 4 个矩阵,宽度和高度分别为:4 * 3,4 * 2,4 * 4,2 * 2
矩阵按高度降序排列,以确保高度相近的矩阵能够一起正确处理。
构造叶子节点:选取高度最高的一批矩阵
4 * 3,4 * 2,4 * 3,把它们的第 1 行拼在一起,哈希后作为第 1 个叶子节点;第 2 行拼在一起,哈希后作为第 2 个叶子节点;依次类推。L0 = layer_digest[4] = Hash(x00, x01, x02, w00, w01, v00, v01, v02, v03) L1 = layer_digest[5] = Hash(x10, x11, x12, w10, w11, v10, v11, v12, v13) L2 = layer_digest[6] = Hash(x20, x21, x22, w20, w11, v20, v21, v22, v23) L3 = layer_digest[7] = Hash(x30, x31, x32, w30, w11, v30, v31, v32, v33)构建后续层:每层的长度为前一层的一半。首先压缩前一层中的元素,如果出现与当前层高度匹配的矩阵,则它们的行也会包含在压缩中。
比如构造第 2 层时出现 2 * 2 的新矩阵 M3,对该矩阵的行进行顺序哈希处理,从而生成一个包含两个摘要的新层。同时,该算法通过压缩第 1 层来创建第 2 层。然后,第 2 层将与 M3 进行顺序哈希运算后生成的新摘要进行进一步压缩。
next_layer_digest[2] = compress(prev_layer_digest[4], prev_layer_digest[5]) tallest_digest = Hash(x00, x01) next_layer_digest[2] = compress(next_layer_digest[2], tallest_digest) next_layer_digest[3] = compress(prev_layer_digest[6], prev_layer_digest[7]) tallest_digest = Hash(x10, x11) next_layer_digest[3] = compress(next_layer_digest[3], tallest_digest)
如果当前高度没有矩阵,则过程简化:
next_layer_digest[1] = compress(prev_layer_digest[2], prev_layer_digest[3])Open Batch
输入
- index:需要打开的叶子节点索引
- prover_data:包含多个矩阵的 MMCS
输出
- openings:是一个向量,第 i 个元素是第 i 个矩阵 M[i] 的第 j 行
j = index >> (log2_ceil(max_height) - log2_ceil(M[i].height))
- proof:叶子节点索引 index 的默克尔路径证明
示例演算
假设
- max_height = 4(log_max_height = 2)
两个矩阵:
- matrix1:高度 4(log2_height = 2)
- matrix2:高度 2(log2_height = 1)
- index = 3(二进制 11)
步骤
计算 openings:
- matrix1:j = 3 >> (2 - 2) = 3,提取第 3 行
- matrix2:j = 3 >> (2 - 1) = 1,提取第 1 行
计算 proof,各层的兄弟节点索引为 sibling hash:
- 第 0 层:(11 >> 0) ^ 1 = 11 ^ 1 = 10(2)
- 第 1 层:(11 >> 1) ^ 1 = 01 ^ 1 = 00(0)
Verify Batch
输入:commit (root), dimensions, index, openings, proof
过程:将 openings 和 proof 里的 sibling hash 逐层合成,最终比对根 hash 是否等于 commit


没有评论