算术化:将计算问题转换为有限域 F 上的多项式代数问题。
zkSTARK 算数化会构建程序的代数中间表达 (Algebraic Intermediate Representation, AIR),用 s 个多项式描述当前执行状态与下一步状态的转换约束。
算术化中会得到两种 witness:
- 整个待证明程序的执行轨迹 execution trace,对应迹多项式。轨迹可以看着一组寄存器的状态转换过程,是基于状态转换表格中的列构造出的多项式。
- 在执行过程中需要满足的约束条件 constraint,对应商多项式。约束包括两部分,边界约束和状态转换约束。
接下来对执行迹和约束条件做多项式承诺,用 FRI 证明商多项是低阶的。迹多项式没有被证明为低阶,这不会降低安全性,因为它的低阶性是由商多项式的低阶性所隐含的。
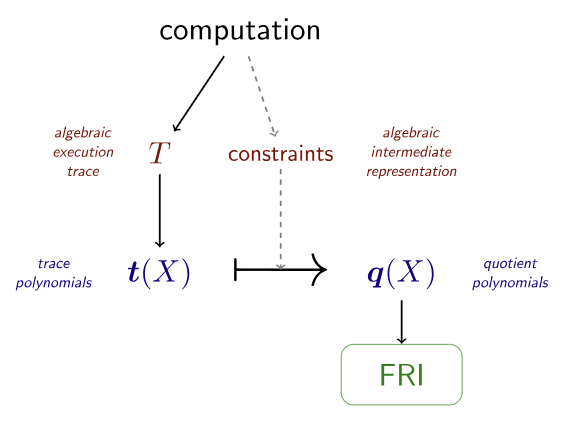
图片来源:Anatomy of a STARK, Part 1: STARK Overview
1 Setup
得到 preprocess trace 及承诺,承诺方式见 2.1。prover 和 verifier 都需要运行。
2 Prove
2.1 Commit
生成 main trace,并对所有 main trace 承诺。main trace 中不包含 lookup 列。
得到 $T$ 行 $w$ 列的 trace 表后,为找到每列的低次多项式,需对每一列进行插值,横坐标为 $o^i$,$o$ 是阶为 $T$ 的一个子群的生成元,得到的多项式为 trace 多项式。
为了引入冗余抵抗恶意篡改,trace 会被插值到更大的域(例如,从 N 点扩展到 8N 点),但多项式的度仍保持 ≤N−1。一般需要将域扩大 $2^k$ 倍,$k$ 称为爆炸因子(blowup factor),该域称为 LDE 域。
求出 trace 多项式在 LDE 域上的值,以这些值为叶子节点,组成一棵 Merkle 树,root 即为承诺。
步骤如下
调用
coset_lde_batch()计算 LDE:let mut poly = domain.ifft(trace); let extended_domain = domain.get_coset(shift).extend(blowup); let extended_trace = extended_domain.fft(&poly);zkvm-brainfuck 中采用的爆炸因子是 1,即 log_blowup=1,所以新 trace 表的高度是原始的 2 倍(1 << log_blowup)。
- 调用
MerkleTreeMmcs::commit()采用 MMCS (Mixed Matrix Commitment Scheme) 批量承诺多个 LDE:将新 trace 表作为叶子节点构建 Merkle 树,root 即为承诺。
过程详见:Stark101-part1
2.2 Open
步骤如下:
生成 lookup trace
根据 main trace 的承诺计算 lookup 挑战值,用到 LogUp 和 Multiset Hashing
生成 lookup trace 的 Merkle 承诺
用与上一章承诺 main trace 同样的方式承诺 lookup trace。这种两阶段承诺方式符合随机化 AIR 预处理 (Randomized AIR with Preprocessing, RAP)
生成 quotient trace
- 计算商多项式的 domain
- 获取该 domain 上的 trace 点
- 根据 trace 点和约束算出状态转换多项式(evaluations 形式)
- 状态转换多项式除以相应的消失多项式 $Z_{H_i}(X) = x^n - 1$,得到商多项式 $p_i(x) = constraints_i(x) / Z_{H_i}(x)$ (evaluations 形式),即为 quotient trace
- 生成 quotient trace 的 Merkle 承诺
- 根据 quotient trace 的承诺计算挑战值 $\zeta$,得到如下 Merkle 树的打开点 $z$:preprocess,main,lookup 和 quotient
调用 plonky3 的
open()批量打开多个商多项式并生成打开证明:$$ \sum_iα^i⋅\frac{p_i(X)−y_i}{X−z} $$
- $p_i(X)$ 是 evalutions 形式的商多项式
- $y_i=p_i(z)$ 是 Barycentric interpolation 结果,$z$ 是打开点
运行 FRI 协议
- commit phase: 每轮都将多项式的次数折半,并且生成该多项式的 Merkle 承诺。如果 $log(d)$ 轮后终得到一个常数多项式,则可以说明多项式的阶接近于 $d$
- query phase: 提供一组验证者随机选择点的评估,并生成其 Merkle proof,以便让验证者确认每一轮承诺的多项式彼此间是一致的
从而证明多个点的打开值的一致性以及相应多项式的低度性质,确保提交的多项式满足预期约束
3 Verify
步骤如下:
- 根据 quotient trace 的承诺计算挑战值 $\zeta$,得到 Merkle 树的打开点:preprocess,main,lookup 和 quotient
调用 plonky3 的
verify()运行 FRI 验证:- 验证折叠关系:在新值的 Merkle 树同一层上抽取 N 个相关的折叠点,在下一层上抽取一个点,就能验证本层的 N 个点确实按正确的随机数折叠到下一层的同一个点。
- 验证折叠后的多项式的阶
验证多项式是否匹配,确保多项式来源于转换约束、边界约束。验证者自己计算 k 个多项式的值,与证明方计算的值看是否相等,防止证明方承诺一个伪造的低阶多项式。
具体步骤为:
- 重新计算商多项式值 $quotient(\zeta)$,验证与打开点是否想等
- 重新计算约束多项式值 $constraints(\zeta)$
- 验证 $constraints(\zeta) / Z_H(\zeta) = quotient(\zeta)$
参考
Mastering SP1 zkVM design-part 3: Core proof


没有评论