什么是 Sumcheck？

Sumcheck 是一种交互式证明协议（Interactive Proof Protocol, IOP），用于让证明者（Prover）向验证者（Verifier）证明一个多元多项式求和结果的正确性，而无需直接计算所有项。它的核心思想是通过分轮次（rounds）的挑战-响应，将高维求和问题逐步简化为单点验证。

核心应用场景

  • 零知识证明（ZKP）：如 GKR 协议、SNARKs 的底层优化。
  • 计算验证：验证大规模矩阵/多项式运算（如 Tensor 计算、ML 推理）。
  • 区块链：轻节点验证链上计算的正确性（如 Rollups）。

协议流程（以二元多项式为例）

对于一个列表 $L=[y_0, y_1, ..., y_{n-1}]$，$n=2^m$，构造一个多项式 $g(x_m, ..., x_2, x_1)$，是一个 multilinear extension，计算结果为列表 $L$ 中的值：

$$ \begin{align} & g(0, ..., 0, 0)=y_0 \\ & ... \\ & g(1, ..., 1, 1)=y_{n-1} \end{align} $$

例如，$L=[1, 2, 3, 5]$，prover 需要向 verifier 证明 $Sum(L) = 11$。因为列表长度 $n=4=2^2$，所以 $m = 2$。有

$$ \begin{align} & g(0,0)=1\\ & g(0, 1)=2\\ & g(1,0)=3\\ & g(1,1)=5\\ \end{align} $$

所以 $g(x_2,x_1)=1(1-x_2)(1-x_1) + 2(1-x_2)x_1+3x_2(1-x_1)+5x_2x_1=1+2x_2+x_1+x_2x_1$

问题变为 prover 向 verifier 证明 $\sum_{x_2 \in \{0,1\}}\sum_{x_1 \in \{0,1\}}g(x_2, x_1) = 11$

步骤：

  1. 第一轮（对 $x_1$ 求和）

    prover 发送一个关于 $x_1$ 的单变量多项式：

    $$ g_1(x_1)=\sum_{x_2 \in \{0,1\}}g(x_2,x_1) = g(0, x_1) + g(1, x_1) = 4 + 3x_1 $$

    verifier 检查 $11 = g_1(0) + g_1(1) = 4 + 7$，并随机选择 一个挑战值 $r_1=3 \in \text{F}$

  2. 第二轮（对 $x_2$ 求和）

    prover 发送一个关于 $x_2$ 的单变量多项式：

    $$ g_2(x_2)=g(x_2,r_1)=4 + 5x_2 $$

    verifier 检查 ${g_1(r_1)=g_2(0) + g_2(1)}$，并随机选择 一个挑战值 $r_2=7 \in \text{F}$

    $g_1(r_1)=g_1(3) = 13$

    $g_2(0)+g_2(1) = 4 + 9 = 13$

  3. 最终验证

    verifier 检查 $g(r_2,r_1)=g_2(r_2)$

    $g(r_2,r_1) = g(7,3)= 1 + 14 + 3 + 21 = 39$

    $g_2(r_2)=g_2(7)=4 + 35 = 39$

关键数学原理

  • 多项式分解：将多元多项式逐变量分解为单变量多项式。
  • Schwartz-Zippel 引理：若 $g_1(x)$ 是正确的多项式，则随机采样 $r_1$ 时，作弊概率 $≤ \frac{deg(g)}{∣F∣}$
  • 递归简化：每轮将问题维度降低一阶。

复杂度分析

指标成本
证明者计算O(2^n)（初始计算）
验证者计算O(n) 次域运算
通信轮次n 轮（变量数）
通信量O(n⋅deg(g))

应用

应用

下面里例子展示了如何将一般计算映射到 Sumcheck，也称算术化（Arithmetization）。

11.png

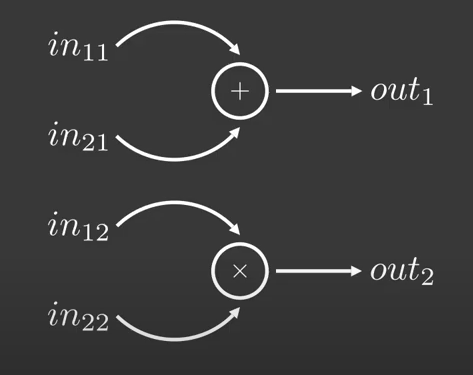
prover 希望证明以上输入输出关系，而无需 verifier 进行实际的计算。

prover 可以构造以下 3 个多项式：

$$ \begin{align} & in_1(x) = in_{11} \cdot (1-x) + in_{12} \cdot x \\ & in_2(x) = in_{21} \cdot (1-x) + in_{22} \cdot x \\ & out(x) = out_{1} \cdot (1-x) + out_{2} \cdot x \\ \end{align} $$

并构造另外两个辅助多项式：

$$ \begin{align} & add(x) = 1 \cdot (1-x) + 0 \cdot x \space \space \space \space\text{Addition Indicatior} \\ & mult(x) = 0 \cdot (1-x) + 1 \cdot x \space \space \text{Multiplication Indicatior} \\ \end{align} $$

以上 5 个多项式组合为如下 prover 想要证明的等式：

$$ add(x) \cdot (in_1(x) + in_2(x)) + mult(x) \cdot (in_1(x) \cdot in_2(x)) = out(x) $$

将以上等式重排列：

$$ add(x) \cdot in_1(x) + add(x) \cdot in_2(x) + mult(x) \cdot in_1(x) \cdot in_2(x) - out(x) = 0 $$

这是一个 Sumcheck 实例，和为 0，也称为 Zerocheck

参考

DeepSeek

Sum-Check 10