Lookup (Log Derivative Lookup Argument) 是一种通过预计算表(Lookup Table)来验证某个值是否存在于特定集合中的技术。在 ZKP 中,它通常用于减少电路约束的复杂性,将复杂的算术约束(如位操作、范围检查)转换为查表操作,减少证明生成的开销。
LogUp 是 Lookup 的一种实现,通过对数组合(Logarithmic Combination)来高效验证多个查询的存在性。
假设 CPU 表如下:
ADD 表如下:
可以看到 ADD 表和 CPU 表中都有加法指令,只是行的顺序不同。对于某条加法指令,CPU 表不作约束,而是交给 ADD 表去约束,但这需要确保 CPU 表的加法指令一定出现在 ADD 表中,这便是 Lookup 协议要证明的。
原理
假设 $n<p$, $p$ 是 K 的特征。如果以下等式成立,则说明矩阵 $\{A_{ij}\}_{i \in [n],j \in [m]}$ 和矩阵 $\{B_{ij}\}_{i \in [n],j \in [m]}$ 相同
$$ \sum^{n-1}_{i=0}\frac{1}{\alpha + \sum^{m-1}_{j=0}\beta^jA_{ij}} = \sum^{n-1}_{i=0}\frac{1}{\alpha + \sum^{m-1}_{j=0}\beta^jB_{ij}} \space \space \space (1) $$
现在做一个变体,我们不想检查 $A$ 的行是否是 $B$ 的行的一个排列,而是对于一个矩阵集合 $A_{ij}^{(1)}, A_{ij}^{(2)}, ..., A_{ij}^{(k)}$,希望证明 $B$ 的任意第 $i$ 行在 $A$ 中出现了 $m_i$ 次。修改 LogUp 协议如下:
$$ \sum^{k}_{l=1}\sum^{n-1}_{i=0}\frac{1}{\alpha + \sum^{m-1}_{j=0}\beta^jA_{ij}^{(l)}} = \sum^{n-1}_{i=0}\frac{m_i}{\alpha + \sum^{m-1}_{j=0}\beta^jB_{ij}} $$
prover 需要对 $m_i$ 承诺。
协议如下:
- prover 承诺 $A, B, m$
- verifier 发送随机元素 $\alpha, \beta \in$ K
prover 发送 $s_i^{(l)}, r_i$
$$ \begin{align} &s_i^{(l)} = \frac{1}{\alpha + \sum^{m-1}_{j=0}\beta^jA_{ij}^{(l)}} \\ &r_i = \frac{m_i}{\alpha + \sum^{m-1}_{j=0}\beta^jB_{ij}} \end{align} $$
verifier 检查
$$ \begin{align} &s_i^{(l)}(\alpha + \sum^{m-1}_{j=0}\beta^jA_{ij}^{(l)})=1 \\ &r_i (\alpha + \sum^{m-1}_{j=0}\beta^jB_{ij})=m_i \end{align} $$
- prover 和 verifier 运行协议来证明 $\sum_ir_i = \sum_{i,l}s_i^{l}$
步骤 4 中两个等式的验证通过添加一个 permutation 列 $\frac{1}{\alpha + \sum_j\beta^jA_{ij}}$ 实现,步骤 5 中等式的验证通过为 $A$ 添加 sum 列 $\sum_{k=1}^ir_k$ 实现,对 $B$ 也类似。这两种等式约束都会被加到 AIR 约束中。最后,CPU 表和 ADD 被扩展如下。
CPU 表:
ADD 表:
以上两表中,$\alpha = 1, \beta = 2$,结果模 7。两个表 Running Sum 列的最后一个元素是相等的。
permutation trace 和 AIR 的代码在这里:https://github.com/felicityin/zkvm-brainfuck/blob/main/crates/stark/src/permutation.rs
内存访问一致性检查
在 zkVM 中,内存访问一致性检查是证明任何读操作返回的值确实是写入该内存地址的最新值。如果能证明读取和写入的数据是置换关系,便可证明内存访问的一致性。
将读取和写入内存改为一对读写操作,读内存改为一对读写操作 (read, write),且 read 和 write 的数据是一致的。写内存也改为一对读写操作 (read, write),但 read 和 write 的数据不一致。除了数据的初始化和最终状态外,中间的 read, write 序列是相同的,可转换为置换关系:
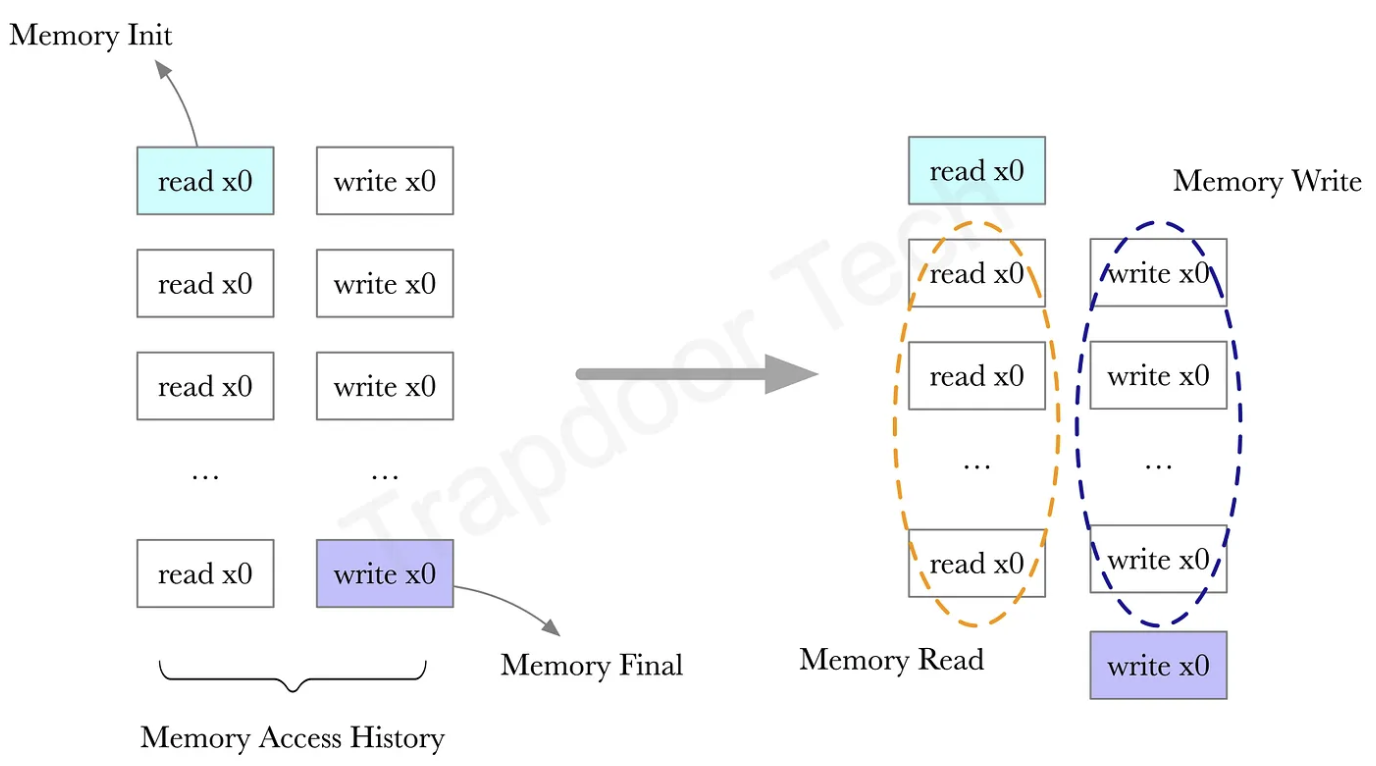
图片来源:Zero Knowledge Proof — Introduction to SP1 zkVM Source Code
中间的 Memory Read 和 Memory Write 序列的置换关系由 CPU 表的 read write 操作之间的 Lookup 来约束。Memory Init 和 Memroy Final 则由 CPU 表和 Memory 表之间的 Lookup 来约束,即 CPU 表会记录对某个地址的所有读写操作,而 Memory 表则只记录对该地址的初始化和最终状态的读写操作。
详细步骤
构造读集合 $R$ 和写集合 $W$,元素都是 $(clk, addr, v)$,分别表示指令周期、地址和值。
初始化:
- $R=W=\emptyset$
- 如果向内存 $addr_i$ 存入初始值 $v_i$,则加到写集合 $W=W\cup\{(0, addr_i, v_i) \}$
内存读取和写入操作:
- 从地址 $addr$ 读值时,找到写集合 $W$ 中最新加入的元素 $(clk_{pre}, addr, v_{pre})$,更新 $R=R \cup \{(clk_{pre}, addr, v_{pre}\}$ 和 $W=W \cup \{(clk_{now}, addr, v_{pre}\}$,其中 $clk_{now}$ 为当前指令周期。
- 将值 $v_{now}$ 写入地址 $addr$ 时,找到写集合 $W$ 中最新加入的元素 $(clk_{pre}, addr, v_{pre})$,更新 $R=R \cup \{(clk_{pre}, addr, v_{pre}\}$ 和 $W=W \cup \{(clk_{now}, addr, v_{now}\}$
后处理:
- 对于所有内存地址 $addr_i$,找到写集合 $W$ 中该地址的最新元素 $(clk_i, addr_i, v_i)$,更新 $R=R \cup \{(clk_{i}, addr, v_{i}\}$
如果最终 $R=W$,便可证明内存访问的一致性。
实现
在 zkvm-brainfuck 的某次运行中,cpu event 和 memory event 示例如下。
cpu event:
[CpuEvent {
...
mp: 0, // 地址
next_mp: 0, // 地址
src_access: Some(Read(MemoryReadRecord { // 读取地址 mp
value: 0, // 数据
timestamp: 1, // 当前的 clk
prev_timestamp: 0 // 上一次的 clk
})),
dst_access: Some(Write(MemoryWriteRecord { // 写入地址 next_mp
value: 1,
timestamp: 2,
prev_value: 0,
prev_timestamp: 1
}))
}, CpuEvent {
...
mp: 0,
next_mp: 0,
src_access: Some(Read(MemoryReadRecord {
value: 1,
timestamp: 4,
prev_timestamp: 2
})),
dst_access: Some(Write(MemoryWriteRecord {
value: 2,
timestamp: 5,
prev_value: 1,
prev_timestamp: 4
}))
}, CpuEvent {
...
mp: 0,
next_mp: 0,
src_access: Some(Read(MemoryReadRecord {
value: 2,
timestamp: 7,
prev_timestamp: 5
})),
dst_access: Some(Write(MemoryWriteRecord {
value: 1,
timestamp: 8,
prev_value: 2,
prev_timestamp: 7
}))
}]其中 src_access 是对地址 mp 的内存操作,dst_access 是对地址 next_mp 的内存操作。本例中,对 mp 都是读操作,对 next_mp 都是写操作。在其它的例子中,对 mp 也可能进行写操作。
memory event:
[MemoryEvent {
addr: 0, // 地址
initial_mem_access: MemoryRecord {
timestamp: 0, // 最初的 clk
value: 0 // 初始化数据
},
final_mem_access: MemoryRecord {
timestamp: 8, // 最终的 clk
value: 1 // 最终的数据
}
}]把 cpu event 中的 src_access 和 dst_access 转成 $(clk, addr, v)$ 形式:
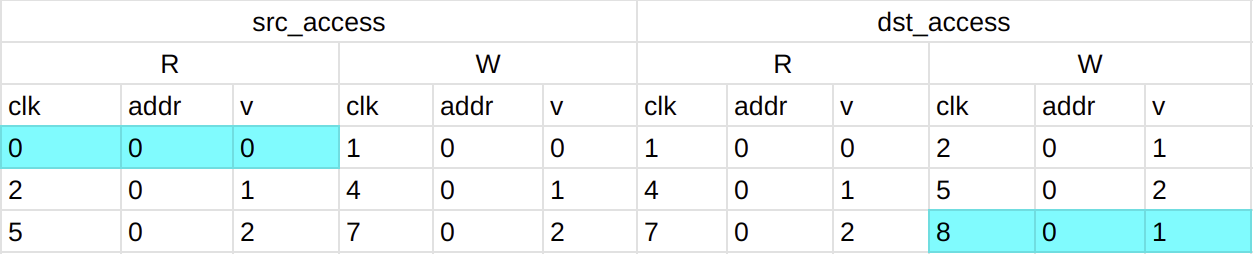
将 $R, W$ 中的元素按照 $clk$ 重新排列,得到如下数据:

将 memory event 也转成 $(clk, addr, v)$ 形式:
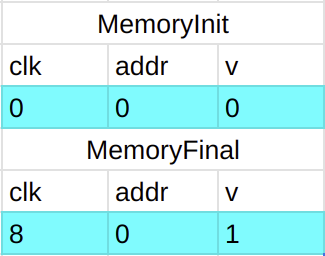
可以看到,如果将 MemoryInit 中的元素加到 $W$ 中,将 MemoryFinial 中的元素加到 $R$ 中,则有 $R=W$,则证明了内存访问的一致性。


没有评论