这篇文章上次修改于 519 天前,可能其部分内容已经发生变化,如有疑问可询问作者。
问题:以太坊使用哈希函数 SHA256/SHA3 计算哈希值,涉及大量的布尔运算和循环操作,需要 2.5 万个 Plonk 门,导致证明生成缓慢。
解决:对于使用频率较高的布尔运算和循环操作
- 预计算一个公开且正确的输入与输出表格 Table
- 证明方使用累加器证明保密数据在该表格 Table 中,则等价于证明:输入和输出的运算是正确的。
Plonkup 核心技术
多项式与集合划分
对整数 $n, d$,向量 $f \in F^n, t \in F^d$。符号 $f ⊂ t$ 指 $\left\{f_i\right\}_{i \in [n]} ⊂ \left\{t_i\right\}_{i \in [n]}$
令 $H = \left\{g, ..., g^{n+1}=1\right\}$ 为乘法子群。
对于保密多项式 $f \in F[X]$,且 $i \in [n+1]$,记为 $f_i = f(g^i)$
当 $f ⊂ t$,如果元素出现在 $f$ 中的顺序与出现在 $t$ 中的顺序相同,则称 $f$ 由 $t$ 划分。形式化表达为,对于任意 $i < i' \in [n]$,有 $f_i \ne f_{i'}$;对于 $j, j' \in [d]$,有 $t_j=f_i,t_{j'}=f_{i'}$,则 $j < j'$
给定 $t \in F^d, f \in F^n, s \in F^{n+d}$,定义 2 个二元多项式: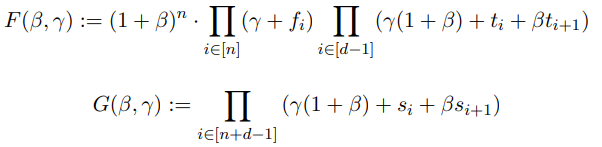
结论:$F ≡ G$ 的充要条件是 $f ⊂ t$ 且 $s=(f,t)$ 由 $t$ 划分
证明:对 $F, G$ 进行如下变换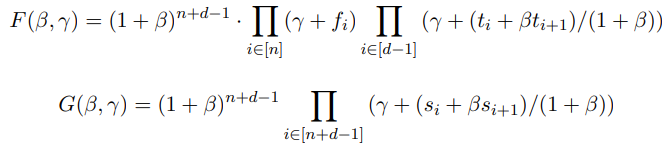
情况 1:如果 $f ⊂ t$ 且 $s=(f,t)$ 由 $t$ 划分:
(1) 对于每个 $j \in [d-1]$,存在一个索引 $i \in [n+d-1]$ 使得
$$ (t_j,t_{j+1}) = (s_j,s_{j+1}) $$
所以有
$$ \gamma + (t_i + \beta \cdot t_{i+1})/(1+ \beta) = \gamma + (s_i + \beta \cdot s_{i+1})/(1+ \beta) $$
相当于 $F(\beta, \gamma)$ 中的 $d-1$ 个元素与 $G(\beta, \gamma)$ 中的 $d-1$ 个元素相等
(2) 接下来证明 $F(\beta, \gamma)$ 中剩余的 $n$ 个元素与 $G(\beta, \gamma)$ 中剩余的 $n$ 个元素相等
令 (1) 中的 $d-1$ 个索引集合记为 $P'⊂ [n+d-1]$,则补集为 $P=[n+d-1]/P'$,则对于剩余的 $n$ 个索引 $i \in P$,有 $s_i=s_{i+1}$,且集合 $\left\{s_i\right\}_{i \in P}$ 等于集合 $\left\{f_i\right\}_{i \in [n]}$
所以有
$$ \gamma + (s_i + \beta \cdot s_{i+1})/(1+ \beta) = \gamma + s_i $$
所以有
$$ \gamma + s_i = \gamma + f_{j(i)} $$
所以 $F ≡ G$ 成立。
情况 2:如果 $F ≡ G$:
(1) 先在 $F$ 中找 $d-1$ 个元素,再在 $G$ 中找 $d-1$ 个元素,它们相等。即
$$ \gamma + (t_i + \beta \cdot t_{i+1})/(1+ \beta) = \gamma + (s_i + \beta \cdot s_{i+1})/(1+ \beta) $$
说明 $t_i + \beta t_{i+1} = s_i + \beta s_{i+1}$,根据 Schwartz-Zippel 引理,得出 $t_i=s_i,t_{i+1}=s_{i+1}$
(2) 对于剩下的 $n$ 个元素,有
$$ \gamma + f_i = \gamma + (s_i + \beta \cdot s_{i+1})/(1+ \beta) $$
说明 $f_i=s_i=s_{i+1}$。因此,有 $f ⊂ t$ 且 $s=(f,t)$ 由 $t$ 划分。
综合情况 1 和情况 2,充要条件成立。
Plookup 原理
预计算公开且正确的 Table 多项式:$t \in F_{< n+1}[X]$
证明方输入的保密多项式:$f \in F_{<n}[X]$
令 $s \in F^{2n+1}$ 为多项式 $f,t$ 的组合 $s=(f,t)$,由 $t$ 划分。使用两个多项式 $h_1,h_2 \in F_{n+1}[X]$ 表达 $s$ 多项式
$$ \begin{align} &h_1(g^i)=s_i, i \in [n+1]\\ &h_2(g^i)=s_{n+i}, i \in [n+1] \end{align} $$
- 证明方计算 $h_1,h_2$ 并发送给可信第三方(证明方对 $h_1,h_2$ 多项式承诺)
- 验证方选择随机数 $\beta, \gamma \in F$ 并发送给证明方(证明方计算哈希值 )
证明方计算多项式 $Z \in F_{<n+1}[X]$,聚合了 $F(\beta, \gamma)/G(\beta, \gamma)$
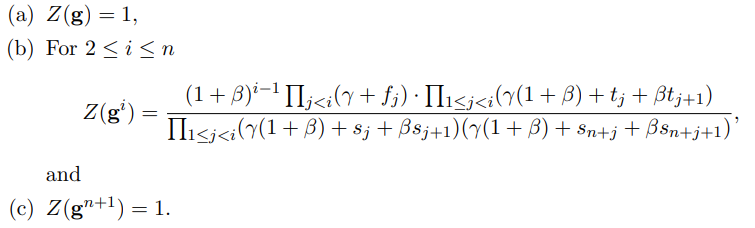
证明方发送 $Z$ 给可信第三方(证明方计算商多项式承诺)。
验证方检测 $Z$ 成功,即 $Z(g^{n+1})=1$。具体而言,对于 $x \in H$,检测如下
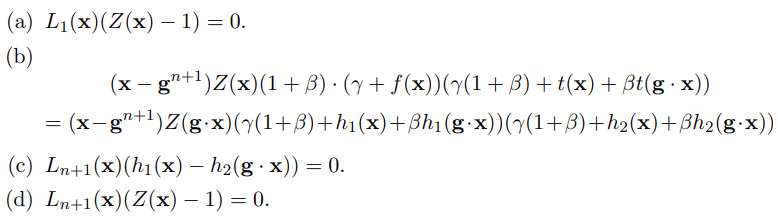
以上 4 个式子都成立则接受,否则拒绝。
证明:
等式 (a) 确保 $Z(g)=1$
等式 (d) 确保 $Z(g^{n+1})=1$
等式 (c) 说明 $h_1(g^{n+1})=h_2(g)$,因此 $h_1,h_2$ 一致的描述了单一向量 $s \in F^{2n+1}$
等式 (b) 是递归项: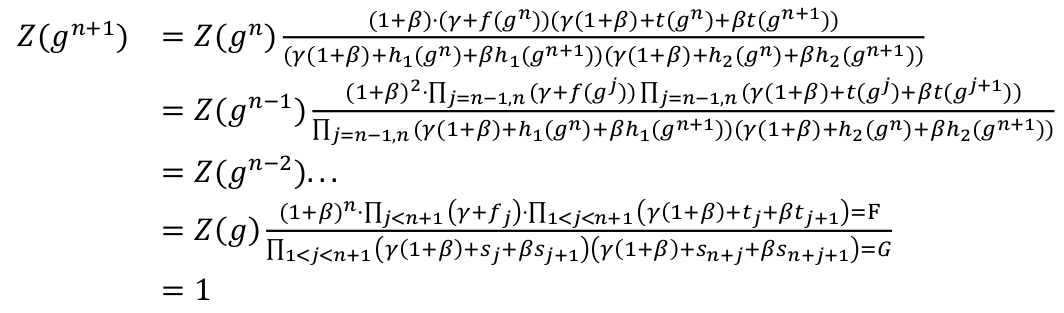
因此,$F ≡ G$,则推导出 $ f ⊂ t$。因此,证明方的 witness 在公开且正确的数据表中,则输入和输出的约束是正确的,则证明方的计算是正确。
Plookup 扩展
对于多个 $f_1, ....,f_w \in F_{<n}[X]$ 和多个 $t_i \in F_{<d}[X]$,其中 $t_i(g^i)=t^*_{i,j}, j \in [d]$
验证方选择随机数 $\alpha \in F$ (证明方计算随机数)
用随机数将多个多项式线性组合规约为一个多项式。
预计算公开且正确的多项式 $t=\sum_{i \in [w]} \alpha^{i} \cdot t_i$
证明方的保密输入多项式 $f=\sum_{i \in [w]} \alpha^{i} \cdot f_i$
然后再用上一节方法证明 $f ⊂ t $
Plookup 范围证明
如果想证明 $ f ⊂ \left\{0,...,d-1\right\}$,其中 $d < n$。可令公开的 Table $t_i=i-1, i \in [d]$ 实现检测。
令 $d=n+1$,可证明 $ f ⊂ \left\{0,...,n\right\}$。还可证明 $f ⊂ \left\{0,...,2n-2\right\}$。将协议一般化,可证明 $f ⊂ \left\{0,...,c(n-1)\right\}$。可令公开的 Table $t=c \cdot (i-1), i \in [n]$ 实现检测。
定义多项式 $P(X)=\sum^{c}_{i=0}(X-i)$
公开的计算多项式:$i \in [n], t_i=c \cdot(i-1)$,预计算多项式为 $t \in F_{<n}[X]$
证明方的保密输入多项式:$f \in F_{<n}[X]$
令 $s \in F^{2n+1}$ 为 $f,t$ 的组合,由 $t$ 划分。使用两个多项式 $h_1,h_2 \in F_{<n+1}[X]$ 表达 $s=(f,t)$
$$ \begin{align} & h_1(g^i)=s_i, i \in [n+1]\\ & h_2(g^i)=s_{n+i}, i \in [n]\\ & h_2(g^{n+1})=c(n-1) \end{align} $$
- 证明方计算多项式 $h_1, h_2$ 并发送给可信第三方(证明方多项式承诺)
- 验证方选择随机数 $\gamma \in F$ 并发送给证明方(证明方计算哈希值)
- 证明方计算多项式 $Z \in F_{<n_1}[X]$,聚合了 $F(\beta, \gamma)/G(\beta, \gamma)$
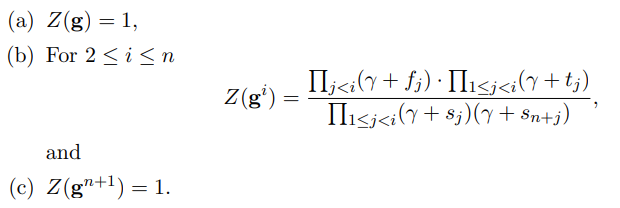
证明方发送 $Z$ 给可信第三方(证明方打开随机点与商多项式承诺) 对于 $x \in H$($H$ 是阶为 $n+1$ 的乘法循环子群,生成元为 $g$),验证:
$$ \begin{align} &(a) L_1(x)(h_1(x))=0\\ &(b) P(h_1(g\cdot x)-h_1(x))=0\\ &(c) P(h_2(g \cdot x) - h_2(x)) = 0\\ &(d) L_{n+1}(x)(h_1(x) - h_2(g \cdot x)) = 0\\ &(e) L_{n+1}(x)(h_2(x)) = c \cdot (n-1)\\ &(f) L_1(x)(Z(x) - 1) = 0 \\ &(g) (x-g^{n+1})(Z(x)(\gamma + f(x))(\gamma + t(x)) = (x-g^{n+1})\cdot Z(g\cdot x)(\gamma + h_1(x))(\gamma + h_2(x))) \\ &(h) L_{n+1}(x)(Z(x)-1) = 0 \end{align} $$
以上 8 个式子都成立,则接受,否则拒绝。
证明:
等式 (a)-(e) 表明 $\left\{h_1(g^i),h_2(g^i)\right\}_{i\in[n]}$ 均在范围 $\left\{0,...,c(n-1)\right\}$ 内
构造多项式
$$ \begin{align} & F(x) = \prod_{i \in [n]}(X-f(g^i))(X-t(g^i))\\ & G(x) = \prod_{i \in [n]}(X-h_1(g^i))(X-h_2(g^i))\\ \end{align} $$
等式 (f)-(h) 表明 $F(\gamma) = G(\gamma)$,推导如下
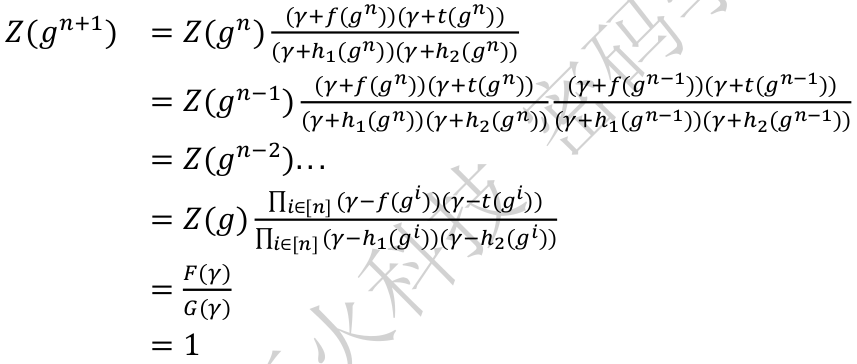
因此,$F ≡ G$。结合冲要条件,则推导出 $f ⊂ \left\{0, . . . , c ⋅ (n − 1)\right\}$。
UltraPlonk
本节涉及的公式较多,省略,详见:zkSnark--UltraPlonk证明系统(下)
公共信息预处理
增加了公开的表格多项式 $T_{1,i},T_{2,i},T_{3,i}, i=1,...,n$
证明过程
- Round1: 不变,计算门数据多项式及承诺
- Round2:计算保密数据多项式 $f(x)$ 和公开的表格数据多项式 $t(x)$。令 $\bar{s}=(\bar{f},\bar{t})$ 由 $\bar{t}$ 划分,将 $\bar{s}$ 拆分为 $\bar{h_1}, \bar{h_2}$,计算对应的多项式 $h_1(x), h_2(x)$。输出 3 个多项式承诺 $[f(x)]_1, [h_1(x)]_1, [h_2(x)]_1$
- Round3:计算线数据多项式 $z_1(x)$ 及承诺 $[z_1]_1$,和公开的 Table 多项式 $z_2(x)$ 及承诺 $[z_2]_1$
Round4:保密数据满足门约束、线约束与查找表。将门约束、线约束和查找表融合到一个多项式 $p(x)$ 中,然后除以目标多项式 $Z_H(x)$ 得到商多项式 $q(x)$
- 第 5 行是选择多项式,确保一些数据等于保密多项式 $f(x)$,这些数据不需要进行标准门约束
- 第 6、7 行是 $z_2(x)$ 的递归约束
- 第 8 行是 $z_2(x)$ 的起始约束
将 $q(x)$ 其拆分为 3 项,并输出 3 个多项式承诺 $[q_{lo}]_1,[q_{mid}]_1,[q_{hi}]_1$
Round5:计算辅助多项式 $r(x)=p(x) - Z_H(x)q(x)$ 的随机打开点。
因为 $r(x)$ 的阶比较高,所以中间还用到了一些多项式值 $f(\xi), t(\xi), t(\omega \xi), z_1(\omega \xi), z_2(\omega \xi), h_1(\omega \xi), h_2(\omega, \xi)$ 等,这些值也要被公开
- Round6:计算商多项式 $W_{\xi}(x),W_{\omega\xi}(x)$,其中 $W_{\xi}(x)$ 还确保 $f(x),t(x),h_2(x)$ 正确,$W_{\omega\xi}(x)$ 还确保 $z_2(x),h_1(x)$ 正确,并输出商多项式承诺 $[W_{\xi}]_1,[W_{\omega\xi}]_1$
最终发送的数据中额外增加了 $[f(x)]_1, [h_1(x)]_1, [z_2]_1, [h_2(x)]_1, f(\xi), t(\xi), t(\omega \xi), z_1(\omega \xi), z_2(\omega \xi), h_1(\omega \xi), h_2(\omega, \xi)$
验证过程
检查承诺的合法性,检查函数值范围的正确性
计算多项式 $r(x)$ 函数值的承诺 $[D]_1$(优化见下一节)。因为 $r(x)$ 阶较高,无法直接计算承诺,所以中间还用到了一个辅助多项式。
计算多项式承诺的线性组合 $[F]_1$
计算函数值的承诺 $[E]_1$
进行双线性验证


只有一条评论 (QwQ)
怎么收藏这篇文章?