这篇文章上次修改于 508 天前,可能其部分内容已经发生变化,如有疑问可询问作者。
零知识证明基础
多项式整除问题
有 3 组阶小于 n 的多项式 $u_0(x),u_1(x),...,u_m(x)$; $v_0(x),v_1(x),...,v_m(x)$; $w_0(x),w_1(x),...,w_m(x)$
一个阶为 n 的目标多项式 z(x), z(x) = 0 有多个解,分别为 $r_1,...,r_n$
对于任意解 $r_j$,3 组多项式的线性组合为 0:
$$ 0 = \left(\sum_{i=0}^ms_i\cdot u_i(r_j)\right) \cdot \left(\sum_{i=0}^m s_i \cdot v_i(r_j)\right) - \left(\sum_{i=0}^ms_i \cdot w_i(r_j)\right) $$
求满足以下整除关系的向量 $\vec{s}=(1, s_1, ..., s_m)$:
$$ z(x) | \left[\left(u_0(x)+\sum_{i=1}^ms_i\cdot u_i(x)\right) \cdot \left(v_0(x)+\sum_{i=1}^m s_i \cdot v_i(x)\right) - \left(w_0(x)+\sum_{i=1}^ms_i \cdot w_i(x)\right)\right] $$
向量 $\vec{s}$ 的维度为 m,如果每一个元素 $s_i$ 的取值空间 > 2,则将线性组合多项式称为二次算法多项式,简称 QAP。如果每个元素的 $s_i$ 的取值空间为 0 或 1,则将线性组合多项式称为二次扩展多项式,简称 QSP
因为 z(x) 为 n 阶,而线性组合多项式的阶为 2n - 2,所以除了 z(x) 还会有 n - 2 个其它解,其它解构成商多项式 h(x)
目标多项式 z(x) 和 QAP/QSP 之间的整除关系满足单向性,不可快速逆向求解。但能快速验证向量 $\vec{s}$ 的正确性,构成 NP 问题。
零知识证明
令 R 为一个高效可计算的二元运算关系。对于二元组 $(x,\omega)\in R$,$x$ 为声明,$\omega$ 为秘密。对于二元运算关系 R,证明系统包含系统参数生成 SysGen,证明 P 和验证 V。
$ZK\left\{\omega|(x,\omega) \in R\right\}$ 包含 5 个多项式时间算法:系统参数生成、承诺、挑战、响应和验证。
$ZK\left\{\omega|(x,\omega) \in R\right\}$ 协议具有如下性质
- 完备性:正确的数据一定被验证通过
- 知识提取鲁棒性:对于同一套随机数生成的 2 个秘密验证 2 次,则验证方可以提取秘密
- 诚实验证方零知识:计算有限,无法提取知识
满足以上性质的 $ZK\left\{\omega|(x,\omega) \in R\right\}$ 协议是一个 $\Sigma$ 协议。
zkSnark 思想
- 证明方:基于向量 $\vec{s}$ 和电路,生成 QAP/QSP 多项式、目标多项式 z(x) 和商多项式 h(x),构造 NP 问题;然后基于这 3 个多项式的系数,计算离散对数点(多项式承诺),对外暴露离散对数点
- 验证方:对离散对数点进行双线性映射,重构整除关系,则能快速验证向量 $\vec{s}$ 的正确性,确不知道向量 $\vec{s}$
zk-SNARK 协议:证明秘密 $\omega$ 满足任意多项式时间计算关系 $y=F(\omega)$
为了不泄露秘密 $\omega$,需要用 R1CS 约束(电路约束)等价描述算法的运算规则。
zk-SNARK 协议的等价转化:
- 将 $\omega$ 满足公开的计算关系 $y=F(\omega)$ 等价转化为 $\omega$ 满足公开的 R1CS 约束
- 等价转化为向量 $\vec{s}$ 与电路多维向量 $u, v, w$ 的内积(基于 $\omega$ 算出 $\vec{s}$,基于 R1CS 约束算出多维向量)
- 等价转化为向量 $\vec{s}$ 与电路矩阵 $U, V, W$ 的内积
- 等价转化为向量 $\vec{s}$ 对 3 组多项式 $U(x), V(x), W(x)$ 的线性组合运算
- 等价转化为目标多项式 z(x) 整除 QAP/QSP 多项式(构成 NP 问题,向量 $\vec{s}$ 放到 QAP/QSP 中)
- 等价转化为基于这 3 个多项式(z(x)、QAP/QSP、h(x))的系数计算椭圆曲线离散对数点(构成零知识),对外暴露离散对数点。
zkSnark 中的转化
多项式时间算法等价转为 R1CS
方程 $x^4+x^3+x^2+x=120$ 可拆分为如下阶为 1 的等式:
$$ \begin{align} & s_1 = x * x \\ & s_2 = s_1 * x \\ & s_3 = s_2 * x \\ & s_4 = s_1 + x \\ & s_5 = s_4 + s_2 \\ & 120 = s_5 + s_3 \end{align} $$
$x=3$ 满足方程的解,等价于 $x=3$ 满足电路约束。
以下术语为等价描述:阶为 1 的等式(Rank 1 Constraint System, R1CS)、R1CS 约束系统、电路约束
以上 6 个阶为 1 的等式包含 3 个乘法门和 3 个加法门,可以将加法约束优化到乘法约束中:
$$ \begin{align} s_1 = x * x \\ s_2 = s_1 * x \\ 120 - (s_2+s_1+x)=s_2 * x \end{align} $$
如果加法门无法耦合到乘法门,则将加法门变为乘法门:
$$ \begin{align} & s_4 = (s_1 + x) * 1\\ & s_5 = (s_4 + s_2) * 1\\ & 120 = (s_5 + s_3) * 1 \end{align} $$
最终R1CS 以乘法们为标准门。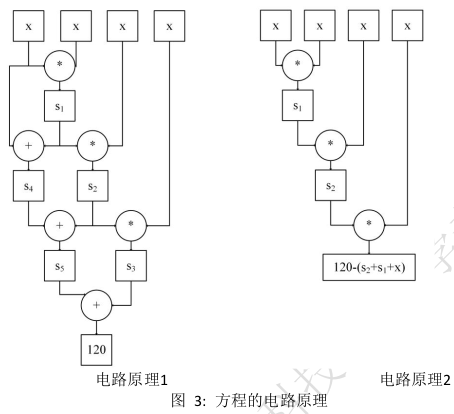
R1CS 转为向量内积
方程的解 $x=3$ 与向量 $\vec{s}$ 等价。
证明:令 $\vec{s}=[1, out, x, s_1, s_2]$。已知 $x=3$,可以逐步算出 $s_1, s_2,out,1$,从而构造向量 $\vec{s}$
公开数据为 statement = (1, out),保密数据为 witness = $(x, s_1, s_2, s_3)$
对于 $s_1=x * x$ 可进行如下向量内积等价转化:
$$ \begin{align} &\vec{s} \cdot [0,0,0,1,0] = [1, out, x, s_1, s_2] \cdot [0,0,0,1,0] = s_1 \\ &\vec{s} \cdot [0,0,1,0,0] = [1, out, x, s_1, s_2] \cdot [0,0,1,0,0] = x \\ &\vec{s} \cdot [0,0,1,0,0] = [1, out, x, s_1, s_2] \cdot [0,0,1,0,0] = x \\ \end{align} $$
令 $w_1=[0,0,0,1,0], u_1=[0,0,1,0,0], v_1=[0,0,1,0,0]$,则有:
$$ \vec{s} \cdot w_1 = \vec{s} \cdot u_1 * \vec{s} \cdot v_1 $$
如下阶为 1 的等式(R1CS 约束)
$$ \begin{align} &s_2=s_1 * x\\ &120-(s_2+s_1+x)=s_2 * x \end{align} $$
可进行如下向量内积等价转化:
$$ \begin{align} &\vec{s} \cdot [0,0,0,0,1] = [1, out, x, s_1, s_2] \cdot [0,0,0,0,1] = s_2 \\ &\vec{s} \cdot [0,0,0,1,0] = [1, out, x, s_1, s_2] \cdot [0,0,0,1,0] = s_1 \\ &\vec{s} \cdot [0,0,1,0,0] = [1, out, x, s_1, s_2] \cdot [0,0,1,0,0] = x \\ \end{align} $$
$$ \begin{align} &\vec{s} \cdot [0,1,-1,-1,-1] = [1, out, x, s_1, s_2] \cdot [0,1,-1,-1,-1] = 120-(s_2+s_1+x) \\ &\vec{s} \cdot [0,0,0,0,1] = [1, out, x, s_1, s_2] \cdot [0,0,0,0,1] = s_2 \\ &\vec{s} \cdot [0,0,1,0,0] = [1, out, x, s_1, s_2] \cdot [0,0,1,0,0] = x \\ \end{align} $$
令 $w_2=[0,0,0,0,1],u_2=[0,0,0,1,0],v_2=[0,0,1,0,0]$; $w_3=[0,1,-1,-1,-1],u_3=[0,0,0,0,1],v_3=[0,0,1,0,0]$,则有:
$$ \begin{align} & \vec{s} \cdot w_2 = \vec{s} \cdot u_2 * \vec{s} \cdot v_2 \\ & \vec{s} \cdot w_3 = \vec{s} \cdot u_3 * \vec{s} \cdot v_3 \\ \end{align} $$
转为向量与矩阵的内积
令
$$ \begin{align} &W = \begin{bmatrix} w_1\\w_2\\w_3 \end{bmatrix} = \begin{bmatrix} 0,0,0,1,0\\0,0,0,0,1\\0,1,-1,-1,-1 \end{bmatrix} \\ &U = \begin{bmatrix} u_1\\u_2\\u_3 \end{bmatrix} = \begin{bmatrix} 0,0,1,0,0\\0,0,0,1,0\\0,0,0,0,1 \end{bmatrix} \\ &V = \begin{bmatrix} v_1\\v_2\\v_3 \end{bmatrix} = \begin{bmatrix} 0,0,1,0,0\\0,0,1,0,0\\0,0,1,0,0 \end{bmatrix} \\ \end{align} $$
则有
$$ \vec{s} \cdot W = \vec{s} \cdot U * \vec{s} \cdot V $$
转为向量对三组多项式的组合运算
将矩阵中的元素当做多项式的值,例如对于矩阵 $W$
$$ \begin{align} &w_0(1)=0,w_1(1)=0,w_2(1)=0,w_3(1)=1,w_4(1)=0\\ &w_0(2)=0,w_1(2)=0,w_2(2)=0,w_3(2)=0,w_4(2)=1\\ &w_0(3)=0,w_1(3)=1,w_2(3)=-1,w_3(3)=-1,w_4(3)=-1\\ \end{align} $$
对于多项式,每列有 3 个函数值,所以取任意 3 个横坐标 $x=1,2,3$,可使用拉格朗日插值或快速傅里叶变换等方式计算多项式的系数。
则多项式系数表达 $W(x)=[w_0(x),w_1(x),w_2(x),w_3(x),w_4(x)]$
同理,有
$$ U(x)=[u_0(x),u_1(x),u_2(x),u_3(x),u_4(x)] \\ V(x)=[v_0(x),v_1(x),v_2(x),v_3(x),v_4(x)] $$
则有
$$ \vec{s} \cdot W(x) - \vec{s} \cdot U(x) * \vec{s} \cdot V(x) = 0, x=1, 2, 3 $$
$U(x)=[u_0(x),u_1(x),u_2(x),u_3(x),u_4(x)]$ 称为向量 $\vec{s}$ 对三组多项式的组合运算,运算结果称为二次算法多项式,简称 QAP 多项式。
目标多项式整除 QAP 多项式构造 NP 问题
上述拉格朗日插值多项式引入横坐标 $x=1,2,3$,则能够构造多项式
$$ z(x)=(x-1)(x-2)(x-3) $$
$z(x)$ 称为目标多项式,也可以选择任意横坐标变量,例如 $x=4,5,6$,则重新使用拉格朗日插值计算函数值,并令 $z(x)=(x-4)(x-5)(x-6)$
当 $x=1,2,3$,目标多项式 $z(x)$ 和 QAP 多项式 $\vec{s} \cdot W(x) - \vec{s} \cdot U(x) * \vec{s} \cdot V(x)$ 均为 0
因为 QAP 多项式阶高于目标多项式 z(x),所以 QAP 还有其它解,所以 z(x) 是 QAP 的因子,换言之,目标多项式 $z(x)$ 和 QAP 多项式为整除关系:
$$ z(x) | (\vec{s} \cdot W(x) - \vec{s} \cdot U(x) * \vec{s} \cdot V(x)) $$
证明方不公开向量 $\vec{s}$,而是使用 $\vec{s}$ 构造出的 QAP 多项式除以目标多项式 z(x),得到商多项式 h(x)
$$ h(x) = (\vec{s} \cdot W(x) - \vec{s} \cdot U(x) * \vec{s} \cdot V(x)) / z(x) $$
然后将 QAP 多项式、目标多项式 z(x) 和商多项式 h(x) 的系数放到椭圆曲线离散对数上(多项式承诺),生成证明(离散对数点)。
验证方获得离散对数点,基于双线性映射重构整除关系,验证了向量 $\vec{s}$ 的正确性,确不知道解向量 $\vec{s}$,即零知识。
zk-SNARK 协议框架
zk-SNARK 协议包括以下 10 个步骤:
- (初始化 a)生成与电路无关的局部系统参数 CRS1
- 证明方 P 证明拥有 $\omega$ 且 $\omega$ 满足任意运算关系 R
- 证明方 P 证明拥有 $\omega$ 且 $\omega$ 满足 R1CS 约束
- 向量 $\vec{s}$ 与多维向量的内积 $\vec{s} \cdot w_i = \vec{s} \cdot u_i * \vec{s} \cdot v_i$
- 向量 $\vec{s}$ 与矩阵 $U, V, W$ 的内积 $\vec{s} \cdot W = \vec{s} \cdot U * \vec{s} \cdot V$
- 向量 $\vec{s}$ 对多项式进行组合运算 $\vec{s} \cdot W(x) - \vec{s} \cdot U(x) * \vec{s} \cdot V(x) = 0$
- 目标多项式 $z(x)$ 整除 QAP 多项式 $z(x) | (\vec{s} \cdot W(x) - \vec{s} \cdot U(x) * \vec{s} \cdot V(x))$ 构成 NP 问题
- (初始化 b)基于电路多项式 $W(x),U(x),V(x)$ 生成局部参数 CRS2
- 证明方 P 将 QAP 多项式、目标多项式、商多项式放到离散对数点上,对外暴露离散对数点 $A, B, C$,实现零知识
- 验证方 V 重构整除关系,验证向量 $\vec{s}$ 的正确性,确不知道向量 $\vec{s}$
Groth16 vs. PLONK
Groth16
CRS 包含 R1CS 等价转化的电路多项式 $W(x),U(x),V(x)$,非常具体
- 优点:证明方 P 使用 CRS 中的电路多项式 $W(x),U(x),V(x)$ 生成证明,速度很快
- 缺点:CRS 包含的电路 $W(x),U(x),V(x)$ 是由 R1CS 转化而来的,已经固化,只能表达唯一运算电路,不能表达其它运算电路,所以表达能力差。如果对 layer2 的电路修改,则步骤 6 中的初始化 b 局部 CRS 也要修改,则 layer1 的合影参数 CRS 也需要修改。
PLONK
CRS 中不包含 R1CS 等价转化的电路多项式 $W(x),U(x),V(x)$,只包含大量的离散对数点。
- 优点:CRS 表达能力强,能够用于任意多项式时间电路生成证明
- 缺点:CRS 表达能力太强,R1CS 约束力不够,不足以防止证明方 P 作弊,所以引入额外的线约束。线约束计算复杂度相对较高,导致证明生成缓慢。
Groth16 协议
初始化 CRS
选择有毒废料随机数 $\alpha, \beta, \gamma, \sigma, x \leftarrow Z_p^*$,计算系统参数 CRS
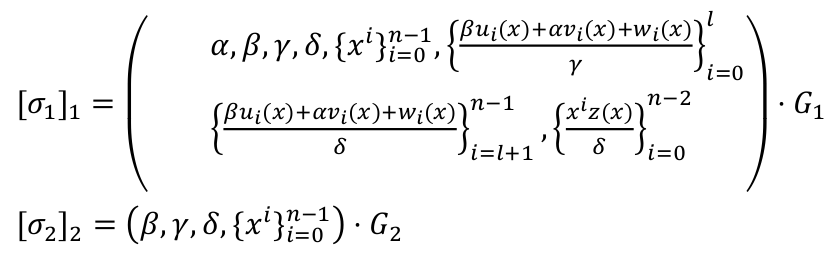
证明方
选择随机数 $r, s \leftarrow Z_p$, $a_0=1$,基于向量 $\vec{s}=(a_1,...,a_m)$ 和 CRS,构造线性组合关系,并将组合多项式的系数放到椭圆曲线离散对数点上,形成离散对数困难问题。对外暴露 3 个离散对数点 $([A]_1, [B]_2, [C]_1)$
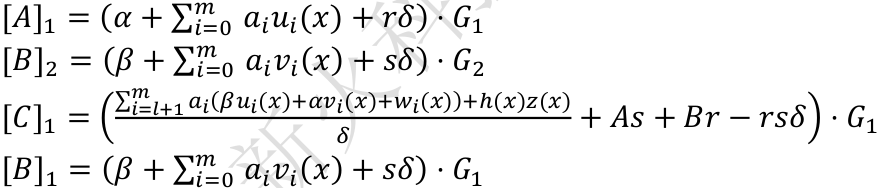
$\alpha, \beta$ 迫使 $A,B,C$ 采用同一条向量 $a_0,...,a_m$ 参数
随机数 $r,s $ 为 $A,B,C $ 增加随机性,否则验证方可以求出 $\vec{s}$
验证方
使用椭圆曲线点重构整除关系
$$ e(A_1, B_2) = e(\alpha G_1, \beta G_2) \cdot e(\sum_{i=0}^l\frac{\beta u_i(x) + \alpha v_i(x) + w_i(x)}{\gamma}G_1, \gamma G_2) \cdot e(C_1, \sigma G_2) $$
推导
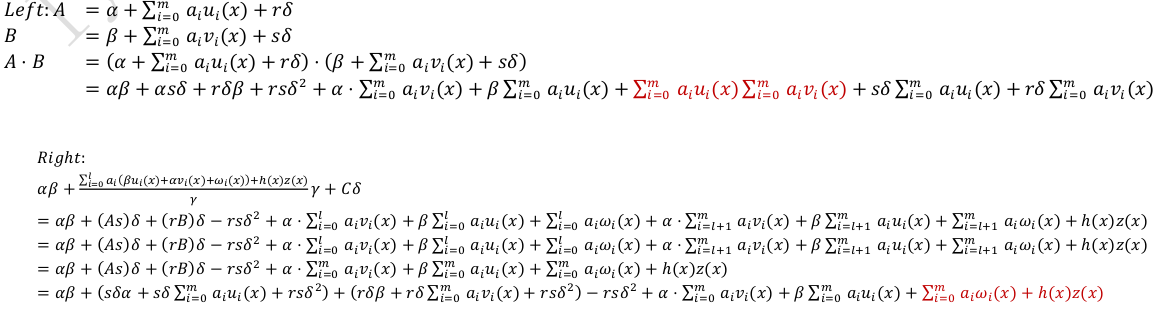
完备性性分析
如果验证方通过了验证,则说明以上红色的部分一定相等,即
$$ \sum_{i=0}^ma_i u_i(x) \sum_{i=0}^m a_i v_i(x) = \sum_{i=0}^ma_i \omega_i(x) + h(x)z(x) $$
则说明 z(x) 与 QAP 多项式 $\sum_{i=0}^ma_i u_i(x) \sum_{i=0}^m a_i v_i(x) - \sum_{i=0}^ma_i \omega_i(x)$ 满足整除关系,则说明证明方知道该 NP 问题的解 $\vec{s}$。
证明方无法作弊
证明方只要修改任意一个参数,都无法使得验证等式成立。
安全性分析
- 从验证方角度,模拟器生成证明与证明方生成证明不可区分。
- 模拟器没有秘密,验证方使用模拟器提供的证明计算不出任何秘密。
- 验证方基于证明方生成的证明,也计算不出任何秘密,实现零知识。


没有评论