这篇文章上次修改于 250 天前，可能其部分内容已经发生变化，如有疑问可询问作者。

哈希函数：将任意长度的消息，映射为一个固定长（256bit）的随机数。这段随机数称为消息摘要。

摘要的长度一般不低于 256 比特。在现实世界的密码学中，算法的安全级别不能低于 128 比特。根据生日悖论，当从 $2^n$ 种可能的空间中随机生成字符串时，在已经生成大约 $2^{n/2}$ 个字符串后，发现碰撞的概率是 50%。所以如果 $2^{128}$ 就是我们想要达到安全目标所要操作的最大次数，就需要产生 256 比特的随机输出。

哈希函数关键性质：

  • 单向性（抗第一原象性）：已知哈希值 Y，无法在多项式时间内计算出哈希原象 X
  • 弱抗碰撞性（抗第二原象性）：已知(X, Y)，无法在多项式时间找到 X’，使得 Y=Hash(X’)
  • 强抗碰撞性（抗碰撞性）：攻击者无法寻找 X, X'，满足 X != X', hash(X) == hash(X)
  • 压缩性：通常是将 512bit 的数据压缩为 256bit；不足 512bit 则填充
  • 随机性：输出的 Y 是 256bit 的 0/1 随机字符串
  • 可重复性：如果输入 x1=x2，则输出的哈希值 Y1=Y2，是函数的基本性质

MD5 和 SHA-1 缺乏抗强碰撞性的能力，已经不安全。

SHA-2 不适合计算秘密消息的哈希值，因为容易受到长度扩展攻击。

NIST 于 2007 年 12 月发表公告，征集新 SHA3 算法。 2010 年 10 月，第 2 轮遴选结束，入选 5 个算法： BLAKE/Grst1/JH/Keccak/Skein，2012 年，Keccak 最终胜出，被命名为 SHA-3。2015 年，FIPS 202 将 SHA-3 指定为新的哈希函数标准。

BLAKE2 是基于 BLAKE 实现的，是主流哈希算法中最快的，定位是安全系数最高的哈希函数。

Poseidon 哈希函数在 64bit 域上进行加法运算、乘法运算，电路门数量较低，是 zk frendly 哈希函数。

1 SHA-2

SHA-2 由 NSA 发明并在 2001 年由 NIST 进行了标准化。SHA2 在设计上借鉴了 SHA-1，有 4 个不同的版本，包括 SHA-224、SHA-256、SHA-384 和 SHA-512。应用非常广泛的是 SHA-256，可提供 128 比特的安全性，对于高度敏感的应用，应使用安全性更强的 SHA-512。

SHA-2 通过迭代调用压缩函数来计算消息的哈希。首先对输入做填充，然后划分为等长的分组，每个分组的长度等于压缩函数的输入长度。然后将压缩函数应用于消息的所有分组，每次迭代中，都将上一轮的输出作为压缩函数的第二个输入参数。

1.1 消息填充

填充的第一个比特为 1，然后补 k 个 0，直到长度满足对 512 取模后余数是 448，剩余 64bit 填充数据长度：

msg' = {msg, 1, 0, ..., 0, msg-len-64bit}

计算方法：(Len(msg) + 1 + k + 64) / 512 = 0，寻找最小自然数 k

注意，信息必须被填充，即使长度已经满足对 512 取模后余数是 448，这时要填充 512 个比特。

1.2 计算摘要

  1. 将消息分解成 n 个 512-bit 大小的块
  2. 对每个块迭代，迭代 n 次后得到 256-bit 的数字摘要

一个 256-bit 摘要的初始值为 $H_0$，与第一个数据块 $M_1$ 运算后得到 $H_1$，即完成了第一个迭代，继续与第二个数据块 $M_2$ 运算得到 $H_2$，...，依次处理，最后得到 $H_n$，即为最终的 256-bit 消息摘要：

$$ H_i = Map(H_{i-1}, M_i) $$

对迭代函数 $Map$ 便是算法的关键，包含了线性变换、非线性变换和轮常量加。

迭代可形象表示为：

31.png
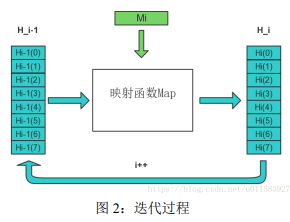
图中 256-bit 的 $H_i$ 被描述 8 个小块，这是因为 SHA256 算法中的最小运算单元称为”字” (Word)，一个字是 32 位。

第一次迭代中，$H_0$ 的来源：对自然数中前 8 个质数（2, 3, 5, 7, 11, 13, 17, 19）的平方根的小数部分取前 32bit

$$ \begin{align} &H_0[0] := 0x6a09e667 \\ &H_0[1] := 0xbb67ae85 \\ &H_0[2] := 0x3c6ef372 \\ &H_0[3] := 0xa54ff53a \\ &H_0[4] := 0x510e527f \\ &H_0[5] := 0x9b05688c \\ &H_0[6] := 0x1f83d9ab \\ &H_0[7] := 0x5be0cd19 \\ \end{align} $$

例如：$ \sqrt{2} $ 小数部分约为 $0.414213562373095048≈6∗16^{−1}+a∗16^{−2}+0∗16^{−3}+...$，质数 2 的平方根的小数部分取前 32bit 就得到 0x6a09e667

Map 映射函数

也就是对称加密中的轮函数 Round Function

Step1 扩展函数

输入：512bits（16个字），输出：2048bits（64个字）

  1. 前 16 个字直接从输入获得：512bit = $W_0, W_1, ..., W_{15}$

  2. 剩余 48 个字由迭代公式得到：$W_t = \sigma_1(W_{t-2}) + \sigma_0(W_{t-15}) + W_{t-16}$

    其中

    $$ \begin{align} &\sigma_0(x) = S^7(x) \bigoplus S^{18}(x) \bigoplus R^3(x) \\ &\sigma_1(x) = S^{17}(x) \bigoplus S^{19}(x) \bigoplus R^{10}(x) \end{align} $$

    其中，$\bigoplus$ 表示按位异或，$S^n$ 表示循环右移 n 个 bit，$R^n$ 表示右移 n 个 bit

Step2 压缩函数

进行 64 次迭代，每次迭代的输入为 64 个常量 $K$ 和 step1 扩展出的 64 个字 $W$，每次迭代如下图所示：

32.png

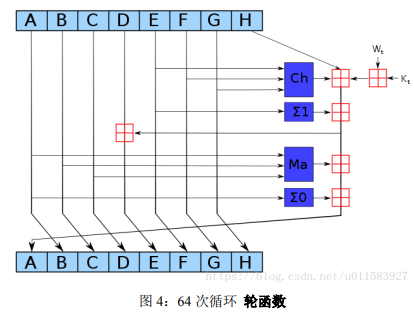
64 个常量 $K$ 来源：对自然数中前 64 个质 数 (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97…) 的立方根的小数部分取前 32 bit

上图中涉及到运算有：

$$ \begin{align} & Ch(x, y, z) = (x ∧ y) \bigoplus (¬x ∧ z) \\ & Ma(x, y, z) = (x ∧ y) \bigoplus (x ∧ z) \bigoplus (y ∧ z) \\ & Σ0 = S^2(x) \bigoplus S^{13}(x) \bigoplus S^{22}(x) \\ & Σ1 = S^6(x) \bigoplus S^{11}(x) \bigoplus S^{25}(x) \\ \end{align} $$

红色的田字方块为：相加后 mod $2^{32}$，其中一个红色方框是字与常量的模加 $W_t + K_t$ (mod $2^{32}$)

ABCDEFGH 的初始值为 $H_0$

2 BLAKE2

BLAKE 由瑞士的 Aumasson 等人设计，采用了 HAIFA 算法迭代结构，其中的压缩算法基于 ChaCha 流密码，内部结构采用 Davies-Meyer 模式，在压缩函数中，采用模余 322 加法运算与 XOR 运算，实现计算的非线性。

BLAKE2 基于 BLAKE 进行了改进，速度和安全性都有所提升。

BLAKE2b 是为 64 为平台设计的，输出 512 bits；BLAKE2s 是为 32 位平台设计的，输出 256 bits。

2.1 消息填充

如果数据库的长度是数据块的整数倍，则最后一个数据块不需要填充，不需要像 BLAKE、MD5 和 SHA-2 那样需要填充数据的长度。

2.2 计算摘要

压缩函数 $F_n(h, m, t, f) = h'$ 输入包括 4 部分：链值 h，消息块 m，计数器 t 和终结标志 f，其中，$h=h_0||...||h_7$，$m=m_0||...||m_{15}$，$t=t_0||t_1$，$f=f_0||f_1$

$f_0, f_1$ 是为了避免如 exploit fixed points 等弱点引入的，作为压缩函数的辅助输入

  • 填充的安全性被转移到终结标志 $f_0$，如果是最后一个数据块，则 $f_0 = \left\{FF...FF\right\}$，否则 $f_0 = \left\{00...00\right\}$
  • 终结标志 $f_1$ 用来在树散列模式中标识最后一个节点，如果是最后一个节点，则 $f_1 = \left\{FF...FF\right\}$，否则 $f_1 = \left\{00...00\right\}$

压缩函数 $F_n$ 包含 3 个步骤：initialization，轮函数 $G$ 和 finalization，包括线性变换、非线性变换、轮常量加

  1. Initialization(h, t, f, IV) = v

$$ v = \begin{bmatrix} v_0 & v_1 & v_2 & v_3 \\ v_4 & v_5 & v_6 & v_7 \\ v_8 & v_9 & v_{10} & v_{11} \\ v_{12} & v_{13} & v_{14} & v_{15} \end{bmatrix} = \begin{bmatrix} h_0 & h_1 & h_2 & h_3 \\ h_4 & h_5 & h_6 & h_7 \\ IV_0 & IV_1 & IV_2 & IV_3 \\ t_0 \bigoplus IV_4 & t_1 \bigoplus IV_5 & f_0 \bigoplus IV_6 & f_1 \bigoplus IV_7\end{bmatrix} $$

​ 其中，

$$ \begin{align} &IV_0 = 0x6a09e667f3bcc908 \space // \space Frac(sqrt(2)) \\ &IV_1 = 0xbb67ae8584caa73b \space // \space Frac(sqrt(3))\\ &IV_2 = 0x3c6ef372fe94f82b \space // \space Frac(sqrt(5))\\ &IV_3 = 0xa54ff53a5f1d36f1 \space // \space Frac(sqrt(7))\\ &IV_4 = 0x510e527fade682d1 \space // \space Frac(sqrt(11))\\ &IV_5 = 0x9b05688c2b3e6c1f \space // \space Frac(sqrt(13))\\ &IV_6 = 0x1f83d9abfb41bd6b \space // \space Frac(sqrt(17))\\ &IV_7 = 0x5be0cd19137e2179 \space // \space Frac(sqrt(19))\\ \end{align} $$

  1. 轮函数 $G(m, v) = v'$

    8 个轮函数 $G_0, ..., G_7$ 执行 10 轮

    输入 512 bit，输出 512 bit

    $G_i$ 的输入和输出可形象地用下图表示：

    39.png

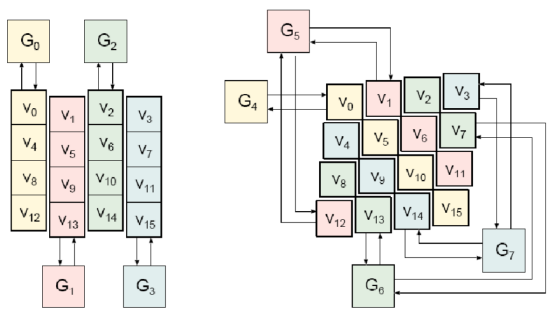
    $$ \begin{align} &[v_0, v_4, v_8, v_{12}] = G_0(v_0, v_4, v_8, v_{12}, m_{\sigma_0}, m_{\sigma_1}) \\ &[v_1, v_5, v_9, v_{13}]=G_1(v_1, v_5, v_9, v_{13}, m_{\sigma_2}, m_{\sigma_3})\\ &[v_2, v_6, v_{10}, v_{14}]=G_2(v_2, v_6, v_{10}, v_{14}, m_{\sigma_4}, m_{\sigma_5})\\ &[v_3, v_7, v_{11}, v_{15}]=G_3(v_3, v_7, v_{11}, v_{15}, m_{\sigma_6}, m_{\sigma_7}) \\ &[v_0, v_5, v_{10}, v_{15}]=G_4(v_0, v_5, v_{10}, v_{15}, m_{\sigma_8}, m_{\sigma_9})\\ &[v_1, v_6, v_{11}, v_{12}]=G_5(v_1, v_6, v_{11}, v_{12}, m_{\sigma_{10}}, m_{\sigma_{11}})\\ &[v_3, v_7, v_8, v_{13}]=G_6(v_3, v_7, v_8, v_{13}, m_{\sigma_{12}}, m_{\sigma_{13}})\\ &[v_3, v_4, v_9, v_{14}]=G_7(v_3, v_4, v_9, v_{14}, m_{\sigma_{14}}, m_{\sigma_{15}}) \\ \end{align} $$

    其中，$\sigma$ 是一个置换矩阵。轮函数 G 将两个输入 $x, y$ 混合为向量 $v$ 中的 4 个字，下标为 $a, b, c ,d$，如下所示：

     FUNCTION G( v[0..15], a, b, c, d, x, y )
   |   v[a] := (v[a] + v[b] + x) mod 2**w
   |   v[d] := (v[d] ^ v[a]) >>> R1 // R1: blake2b 是 32，blake2s 是 16
   |   v[c] := (v[c] + v[d])     mod 2**w
   |   v[b] := (v[b] ^ v[c]) >>> R2 // R2: blake2b 是 24，blake2s 是 12
   |   v[a] := (v[a] + v[b] + y) mod 2**w
   |   v[d] := (v[d] ^ v[a]) >>> R3 // R3: blake2b 是 16，blake2s 是 8
   |   v[c] := (v[c] + v[d])     mod 2**w
   |   v[b] := (v[b] ^ v[c]) >>> R4 // R4: blake2b 是 63，blake2s 是 7
   |   RETURN v[0..15]
 END FUNCTION.

  2. Finalization$(h, v') = h'$ 压缩输出结果

    $$ \begin{align} &h'_0 = h_0 \bigoplus v'_0 \bigoplus v'_8 \\ &h'_1 = h_1 \bigoplus v'_1 \bigoplus v'_9 \\ &h'_2 = h_2 \bigoplus v'_2 \bigoplus v'_{10} \\ &h'_3 = h_3 \bigoplus v'_3 \bigoplus v'_{10} \\ &h'_4 = h_4 \bigoplus v'_4 \bigoplus v'_{12} \\ &h'_5 = h_5 \bigoplus v'_5 \bigoplus v'_{13} \\ &h'_6 = h_6 \bigoplus v'_6 \bigoplus v'_{14} \\ &h'_7 = h_7 \bigoplus v'_7 \bigoplus v'_{15} \\ \end{align} $$

3 SHA3-Keccak

采用海绵结构（sponge construction），在预处理（padding 并分成大小相同的块）后，海绵结构主要分成两个阶段：

  • 吸入阶段（absorbing phase）：将块 $x_i$ 传入算法并处理。
  • 挤出阶段（squeezing phase）：产生固定长度的输出。

这两个阶段使用同一个轮函数 Keccak-f。下图以 8 bit 置换为例，Keccak-f 将大小为 8 bit 的输入随机化为长度相同的输出。输入和输出都分为两部分：比率（长度为 r）和容量（长度为 c）。容量也看作秘密值，容量越大，海绵结构就越安全。

34.png

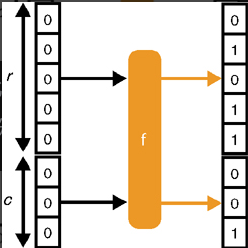
  • r：比特率（bit rate），为每个输入块的长度
  • c：容量（capacity），为输出长度的两倍
  • b：向量的长度，b = r + c，b 的值依赖于指数 L，即 L = 6, b = $25 * (2^L)$ = 1600
  • Keccak-256：b = 1600, r = 1088, c = 512，输出长度为 256，安全级别为 128

为了吸收哈希函数输入的 00101 这 5 个比特，可以使用比率为 5 比特的海绵结构将 5 比特的输入与比率比特（初始化为 0）进行异或，然后将产生的结果作为置换函数的输入，实现对输入的随机化：

35.png

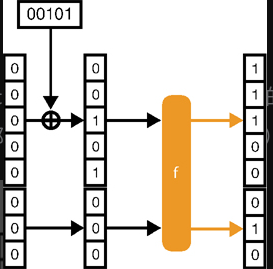
如果想计算更长输入的哈希值，需要

（1）对输入进行填充（如有必要），并将输入分成与比率比特串长度相等的分组。

​ 填充规则：m' = {m, 1000001}，0 的个数 k 为满足 (len(msg) + 2 + k) / r = 0 的最小自然数

（2）迭代调用置换函数，每次将消息分组与置换输入的比率比特串进行异或，然后将中间输出状态输入置换函数，直至处理完所有的消息分组为止：

37.png

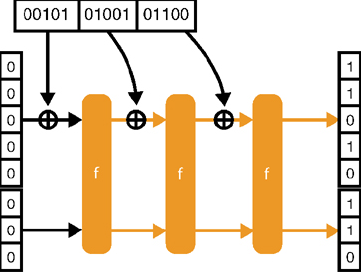
为了产生一个摘要，可以简单地截取海绵结构的最后输出状态的比率比特串（不会使用容量比特串）。为了获得更长的摘要，可以继续读取输出状态的比率比特串部分，然后对其进行置换：

38.png

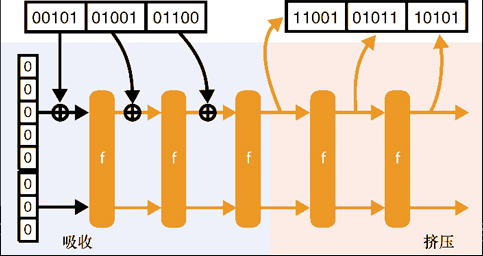
3.1 轮函数

输入为 b = r + c 比特，输出为 b = r + c

40.png

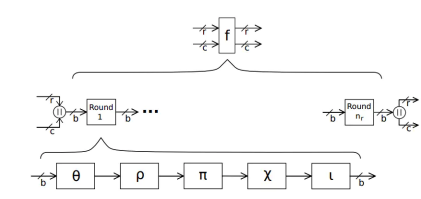
轮函数 Kecaak-f 内部有 5 个变换，前 3 个是线性变换，第 4 个是非线性变换，最后一个是轮常量/轮密钥加

Kecaak-f 包含 n 轮，n 的取值与之前计算 b 时用到的指数 L 成线性关系，对于 Keccak-256，有：

$$ L = log_2W=log_264=6 \\ n=12 + 2L = 24 $$

在每一轮中，执行 θ(theta)、ρ(rho)、π(pi)、χ(chi)、ι(iota)。将 b = 1600 比特数据排列成一个 5 5 64 的立体。

  • AES 加密将数据排为平面矩阵，轮函数包含 4 种操作：字节替代（S 盒子）、行移位、列混淆和轮密钥加。
  • SHA3-Keccak 将数据排为立体，轮函数包括 5 个子函数：θ(theta)、ρ(rho)、π(pi)、 χ(chi)、ι(iota)。

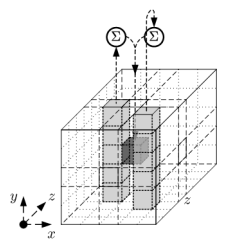
3.1.1 Theta (θ) 函数

二进制的加法运算就是二进制异或

列与周围 2 列元素相加： $a'[x][y][z] = a[x][y][z] + \sum^4_{y'=0}a[x-1][y'][z] + \sum^4_{y'=0}a[x+1][y'][z-1]$

42.png

3.1.2 Rho (ρ) 和 Pi (π) 函数

Rho (ρ) 是在深度方向循环移位：$a'[x][y][z]=a[x][y][z-(t+1)(t+2)/2], t \in [0, ..., 24], (x,y)=(1,0) \begin{pmatrix} 0 & 2 \\ 1 & 3\end{pmatrix}^t$

Pi (π) 是在平面的旋转：$\begin{pmatrix} x'\\y'\end{pmatrix}=\begin{pmatrix} 0 & 1 \\ 2 & 3\end{pmatrix}^t\begin{pmatrix} x\\y\end{pmatrix}, t=0,...,23$

Rho (ρ) 和 Pi (π) 结合成一个式子，相当于深度方向的移位和平面的旋转同时进行。

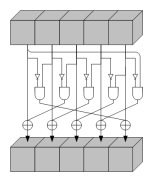
3.1.3 Chi (χ) 函数

唯一的非线性变换，将某一行的数据与后面两行数据累加

For x=0,…,4 {
    For y=0,…,4 {
        a’[x][y]= a[x][y]⊕(NOT a[x+1][y]) AND a[x+2][y]
    }
}

43.png

3.1.4 iota (ι) 函数

异或轮函数，消除对称性：$a’[0][0]= a[0][0] ⊕ RC, z=0,…,23$

其中，RC 是常量，值与轮数有关

4 Poseidon 哈希函数

Poseidon 哈希函数在 64bit 域上进行加法运算、乘法运算，电路门数量较低，是 zk frendly 哈希函数。

初始向量：$I=0^r||0^c$，r-bit 的 0 和 c-bit 的 0

将数据分为多个块，例如 4 块 $m=\left\{m_1 || m_2 || m_3 || m_4\right\}$，输出 $h=\left\{h_1 || h_2\right\}$

44.png

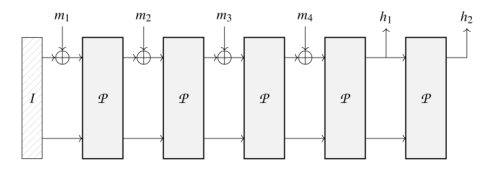
Poseidon 的轮函数包括：

  • 轮密钥/常量加（添加常量）
  • 非线性变换（S 盒子） $S-box( x ) = x^5$
  • 线性变换（MDS 矩阵/满秩） $\vec{m'} = A \cdot \vec{m}$

参考

【新火公开课】密码学基础系列课程1: 对称加密与哈希函数

戴维-王. 深入浅出密码学[M]

BLAKE2: simpler, smaller, fast as MD5

rfc7693

Indifferentiability_of_the_Hash_Algorithm_BLAKE

BLAKE2 简介