这篇文章上次修改于 718 天前,可能其部分内容已经发生变化,如有疑问可询问作者。
本文整理自 BIP32-Compatible Threshold Wallets
目标
设计一个兼容 BIP32 的 HD 钱包,以支持门限 $(t, n)$ 签名。在推导子钱包的过程中无需交互。
non-hardended 和 hardened 钱包的区别是能否从父公钥推出子公钥,前者可以,后者不能。
non-hardened 钱包都是门限的,例如对于门限 $(t, n)$,任意 $t + 1$ 方子私钥分片可算出共享子私钥或进行签名。
hardened 钱包是非门限的,因为被攻破后不会影响剩余钱包的安全性。
non-hardened 节点和 hardened 节点的父节点都是 non-hardened 节点,hardened 钱包只能位于叶子节点。
定义
TVRF
一个非交互式的 $(t,n)$ TVRF(threshold verifiable random function )为 TVRF = (Gen, PEval, Combine, Verify)
- $Gen(1^k, t, n)$
- $\phi_i, \pi_i \leftarrow PEval(m, sk_i, pk)$
- $\phi \leftarrow Combine(pk, m, S, \left\{\phi_i, \pi_i\right\}_{i \in S})$
- $Verify(pk, m, \phi, \pi)$
RTSig
拥有重随机 key 的交互式门限签名为 RTSig = (Gen, RandSK, RandPK, TSign, Verify),其中 (Gen, TSign, Verify) 是 $(t,n)$ 门限签名中原有的算法
将 GG[H$_0$](如 gg18、gg20)扩展为 rGG[H$_0$]:

RandSK 可以确定性的算出 $t$ 度多项式。$sk'_i \leftarrow sk_i + \rho_i$ 是共享私钥 $sk + \rho$ 的分片。
为了确保安全,签名的时候需要同时对 $(pk, m)$ 签名,而不仅仅是对 $m$ 签名。
Non-Hardened 推导
一个 non-hardened 父节点可推出门限 non-hardened 子钱包。
每个父设备都会存储私钥分片 $sk_{i,ID}$ 和 chaincode $ch_{ID}$,在本地计算:
$(\rho, chi_{ID'}) \leftarrow H(pk_{ID}, chi_{ID}, ID')$
根据共享公钥、chain code 和下标算出增量和子 chain code
$sk_{i,ID'} \leftarrow rGG[H_0].RandSK(i, sk_{i,ID}, \rho)$
根据私钥分片和增量算出新私钥分片
父节点将 $sk_{i,ID'}$ 和 $chi_{ID'}$ 发送给 $n$ 个子节点
对于门限 $(t, n)$,每个子节点应收到任意 $t+1$ 个父节点算出的 $sk_{i,ID'}$ 和 $chi_{ID'}$
发送 $chi_{ID'}$ 比较容易,因为 chain code 本来就是公开的
发送 $sk_{i,ID'}$ 比较复杂,因为不能泄露值,否则可反推出共享子私钥,应采用 DPSS(dynamic proactive secret sharing)模式发送
Hardened 推导
回忆一下,hardened 推导是从父私钥推出子公/私钥增量,但对于门限钱包,出现父私钥是很不安全的。
为了避免从共享父私钥算出增量,可以让父节点一起分布式算出确定性随机值,但该随机值只有子节点知道,父节点不知道。子节点可根据该随机值算出子私钥分片。
为了让 $n$ 方计算随机值,采用 TVRF(threshold verifiable random function )。对于 $(t,n)$-TVRF,每方都有一个私钥分片 $sk_i$,可基于消息 $m$ 算出共享值 $\phi_i$ 和 proof $\pi_i$,任意 $t+1$ 方可算出 $\phi$ 和 $\pi$,任意一方可验证 $\phi$ 是否正确。
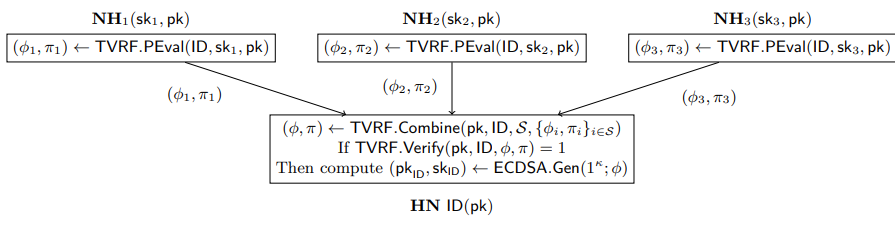
上图展示了门限 hardened 推导。每个 non-hardened 设备 $NH_i$ 都会存储 TVRF 公钥 $pk$ 和私钥分片 $sk_i$。为了推出 hardened 节点 $HN$,每个 non-hardened 设备会在本地算出 $\phi_i, \pi_i$,然后发给 $HN$,$HN$ 收到任意 $t+1$ 个 $\phi_i, \pi_i$ 便可算出 $\phi, \pi$,并进行验证,然后将 $\phi$ 作为 ECDSA keygen 的输入,算出 $pk, sk$。
改善:TVRF 可以与 ECDSA 采用同一个公私钥对,可减少交互轮数,节省存储空间,并且仍然安全。


没有评论