这篇文章上次修改于 807 天前,可能其部分内容已经发生变化,如有疑问可询问作者。
问题描述
通过如下关系去计算一个序列
$$ \begin{align} & a_0 = 3 \\ & a_{n+1} = a_n^2 \\ \end{align} $$
结果需要模一个素数 17,得到前 4 个元素 {3, 9, 13, 16}
生成 trace 多项式

算出 $a_0 = 3, a_1 = 9, a_2 = 13, a_3 = 16, ...$
使用 g = 13 得到 $D_t = \left\{13^0, 13^1, 13^2, 13^3 \right\} = \left\{1, 13, 16, 4 \right\}$。$13^4$ mod 17 = 1 又会等于第 1 个元素。
根据 $D_t$ 到 $a_n$ 的映射关系 $t(g^n) = a_n$ 得到 $t(1) = 3, t(13) = 13, t(16) = 13, t(4) = 16 $
利用拉格朗日插值,得到 trace 多项式 $t(x) = 13x^3 + 2x^2 + 16x + 6$
承诺 trace 多项式
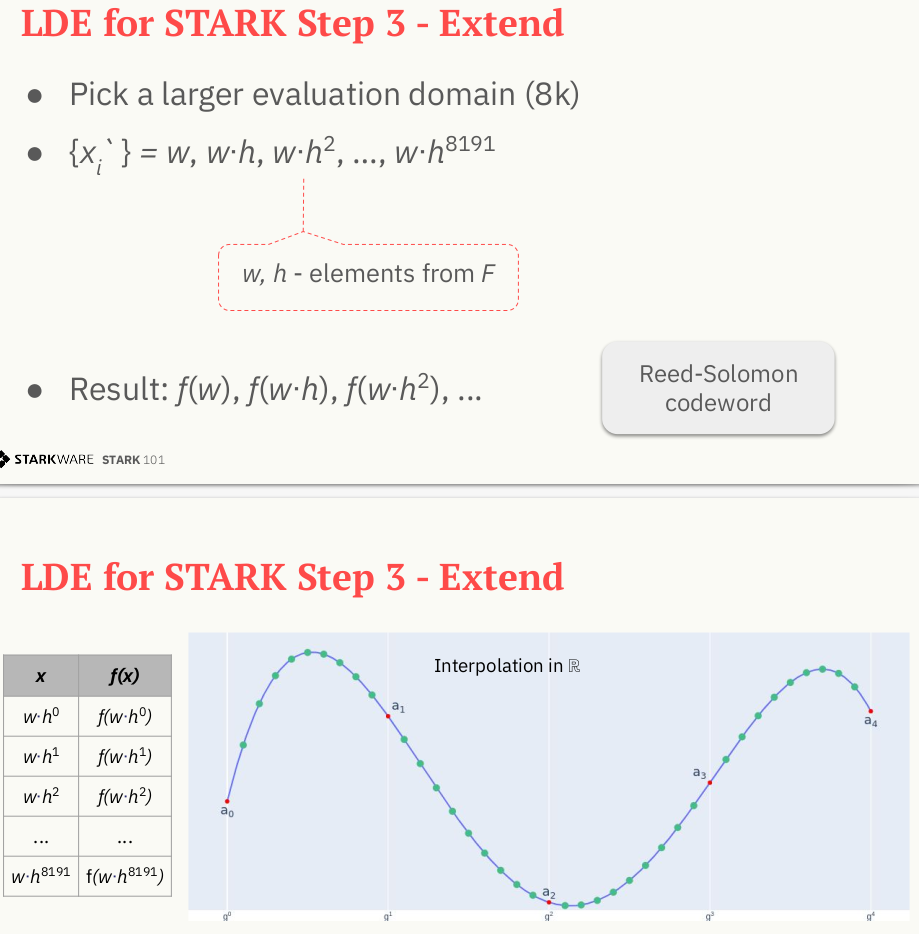
先进行低域扩展(LDE,low-degree extension),得到一个与之前不同的域。如果选择 $h=9$,得到循环群 $\left\{h^0, h^1, .., h^7 \right\}$,这个群包含了 $D_t$ 中的元素,所以通过使用一个 coset 中的元素 $w$ 来移动该域,得到
$$ D_0 = \left\{wh^0, wh^1, .., wh^7\right\} $$
使用 $w=3$ 得到
$$ D_0 = \left\{3, 10, 5, 11, 14, 7, 12, 6\right\} $$
就可算出 $t(x)$ 在 $D_0$ 上的值,使用这些值就可以构建出 Merkle tree。
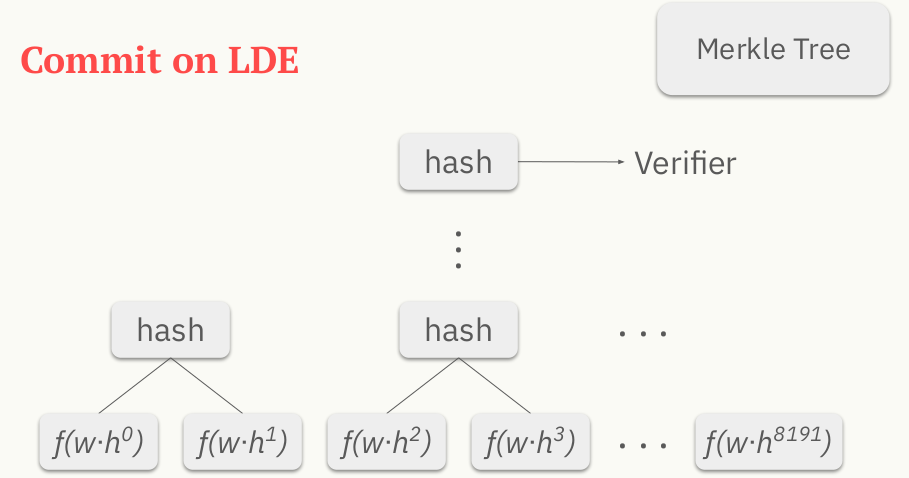
改写约束
需要在 trace 多项式计算值,有两个约束
- 边界约束:$ t(1) = 3 $
- 递归约束:$P(x, y) = y - x^2, \space x = a_n, y = a_{n+1} $
边界约束
$$ p_1(x) = t(x) - 3 = 13x^3 + 2x^2 + 16x + 3 $$
背景知识:要证明 $p(1) = 3$,只需需证明 $r(x) = p(x) - 3$ 可被 $x-1$ 整除
可以得到
$$ C_1(x) = \frac{p_1(x)}{x-1} = 13(x^2 + 9x + 5) $$
递归约束
因为 $D_t$ 是通过生成元 $g=13$ 生成的,所以当 $x=x_0$ 时,$y=gx_0$ 就是下一个元素,所以
$$ \begin{align} & y = t(gx) = t(13 x) = x^3 + 15x^2 + 4x + 6 \end{align} $$
替换 $P(x, y)$,得到
$$ \begin{align} p_2(x) = P(t(x), t(gx)) = x^6 + 16x^5 + 5x^4 + 2x^3 + 7x^2 + 16x + 4 \end{align} $$
当 $x \in 1, 13, 16$ 时,该多项式为 0。因为 $a_{n+1} = a_n^2$,所以对于 $D_t$ 中的最后一个元素 $4$ 没有下一个元素,所以根没有 4。
所以得到 $Z_2(x) = (x-1)(x-13)(x-16)$,又因为 $x^4 = 1$,所以 $Z_2 = \frac{x^4-1}{x-4}$
所以
$$ C_2(x) = \frac{p_2(x)}{Z_2(x)} = x^3 + 12x^2 + 9x + 16 $$
多项式组合
得到多项式
$$ H(x) = C_1(x)(\alpha_1x^{D-D_1} + \beta_1) + C_2(x)(\alpha_2x^{D-D_2} + \beta_2) $$
$\alpha_k, \beta_k$ 由 verifier 提供。$D - D_k$ 是为了让所有的多项式有相同的度,希望度是 2,所以 $D = 4$
例如选择 $\alpha_1 =1, \beta_1 = 3, \alpha_2 = 2, \beta_2 =4$ 后就可以算出 $C_1(x), C_2(x)$,进而算出
$$ H(x) = 15x^4 + 9x^3 + 11x + 4 $$
根据 $H(x) = H_1(x^2) + xH_2(x^2)$ 得到
$$ H_1(x^2) = 15x^4 + 4 \\ H_2(x^2) = 9x^2 + 11 $$
在域 $D_0$ 上计算出 $H_1(x)$ 和 $H_2(x)$ 就可以得到两棵 Merkle tree
verifier 验证
verifier 在 trace 和评估域外,比如 {2, 8, 9, 15},选择随机点 $z$,比如 8,算出
$$ H(8) = 10, H_1(8^2) = 6, H_2(8^2) = 9 $$
因为需要算出组合多项式和 trace 多项式是相关的,所以还需要算出 $t(x)$ 和 $t(gx)$,即
$$ t(8) = 16, t(13 * 8) = 14 $$
验证中的计算:
$$ \begin{align} & p_1(8) = t(8) - 3 = 13 \\ & Z_1(8) = 8 - 1 = 7 \\ & C_1(8) = p_1(8)/Z_1(8) = 14 \\ & C_1(8)(1 \times 8^2 + 3) = 3 \\ \\ & p_2(8) = t(2) - t(8)^2 = 13 \\ & Z_2(8) = 8 \\ & C_2(8) = p_2(8)/Z_2(8) = 8 \\ & C_2(8)(2 \times 8 + 4) = 7 \\ \\ & H(8) = C_1(8) + C_2(8) = 10 \end{align} $$
所以 $H(z) = H_1(z^2) + xH_2(z^2)$。
避免 prover 作弊
verifier 要如何验传过来的值确实是在 $z$ 和 $gz$ 处算出来的?还是使用相同的方式,要证明 $p(a) = b$,只需需证明 $p(x) - b$ 可被 $x-a$ 整除。得到如下深度组合多项式:
$$ \begin{align} P_0(x) = & \gamma_1\frac{t(x)-t(z)}{x-z} + \gamma_2\frac{t(x)-t(gz)}{x-gz} + \gamma_3\frac{H_1(x^2)-H_1(z^2)}{x-z^2} + \gamma_4\frac{H_2(x^2)-H(z^2)}{x-z^2} \\ & = 15x^3 + 15x + 1 \end{align} $$
在域 $D_0$ 上算出 $P_0(x)$ 的值,可根据算出的值构建 Merkle tree。
将 $P_0(x)$ 分割成奇数和偶数部分:
$$ \begin{align} & xP_{0, odd}(x) = 15x^3 + 15x \\ & P_{0, even}(x) = 1 \end{align} $$
verifier 使用 $\beta_0 = 4$,得到 $P_1(y=x^2) = 9y + 10$,$D_1 = \left\{9, 15, 8, 2 \right\}$,可得到 $P_1(y)$ 的 Merkle tree。
重复该过程:
$$ \begin{align} & yP_{0, odd}(y) = 9y \\ & P_{0, even}(y) = 10 \end{align} $$
verifier 使用 $\beta_1 = 3$,得到 $P_2(z=y^2) = 3$,$D_2 = \left\{13, 4 \right\}$,得到一个常量多项式。
prover 需要构建的 Merkle tree 有:trace 多项式、组合多项式、组合多项式的下级等: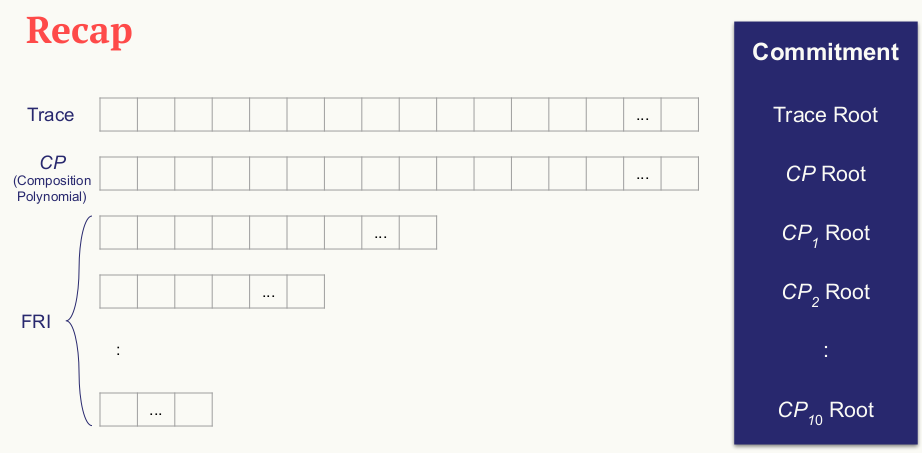
FRI 检查
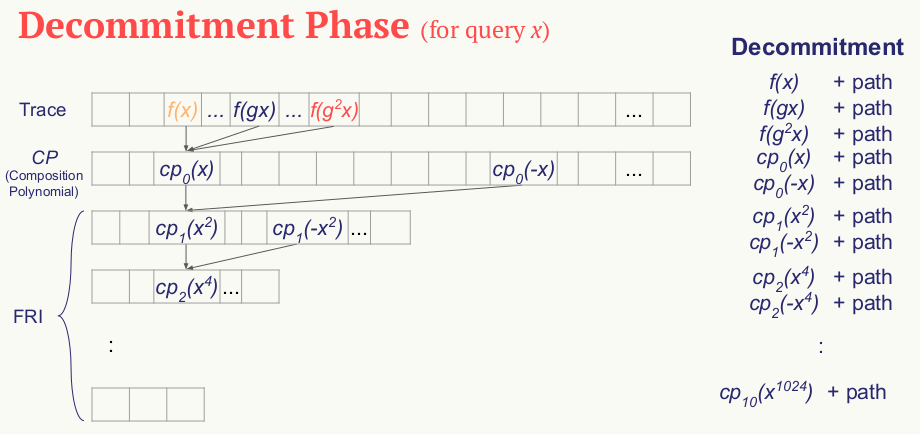
注:以上图片和下面的文字不一定对应,其实不需要 $f(g^x)$
为了生成 proof,verifier 从 $D_0$ 选择一个元素。prover 需要发送重建组合多项式和 FRI 步骤的所有元素。
比如 verifier 选择了 $x=10$,相应的下标是 1。prover 需要发送每层 $x, -x$ 处的值和 trace 多项式在 $x, gx$ 处的值。
对于 $P_0(x)$,发送 $P_0(x=10)=4$ 和 $P_0(x=7)=15$,以及相应的 Merkle proof
对于 $P_1(x)$,发送 $P_1(x=15)=9$ 和 $P_1(x=2)=11$,以及相应的 Merkle proof
对于 $P_2(x)$,只需要发送常量 3
根据 Merkle tree 和如下式子检查 FRI
$$ P_{i+1}(x^2) = \frac{P_i(x) + P_i(-x)}{2} + \beta_i\frac{P_i(x) - P_i(-x)}{2x} $$
检查第一层:
$$ P_1(15) = 9 = \frac{P_0(10) + P_0(7)}{2} + 4\frac{P_0(10-P_0(7))}{2 \times 10} = 1 + 8 $$
检查下一层:
$$ P_2(4) = 3 = \frac{P_1(15) + P_1(2)}{2} + 3\frac{P_1(15)-P_1(2))}{2 \times 15} = 10 + 10 $$
个人理解
以下部分纯属个人理解,可能不对,欢迎指正。
将
$$ \begin{align} & a_0 = 3 \\ & a_{n+1} = a_n^2 \\ \end{align} $$
转换为如下式子对应于 plonk 中的门约束
$$ \begin{align} & z - 3 = 0 \\ & y - x^2 = 0 \end{align} $$
生成 trace 多项式的过程对应于 plonk 中的预处理
$$ t(g^n) = a_n $$
plonk 中把门转为多项式后,交给 FRI 证明
FRI 的通用输入是一个多项式
$$ H(x) = \alpha_1C_1(x) + \alpha_2C_2(x) $$
FRI 会把多项式转为 RS code,RS[F, $S$, $ρ$],表示一组低度多项式 $f : S → F$,它们的度 $d < ρN$,然后用递归的方式证明原多项式不会离 RS code 太远,并且低度多项式是对的。
参考
Diving DEEP FRI in the STARK world: learning your daily moon math with a concrete example


没有评论