这篇文章上次修改于 843 天前,可能其部分内容已经发生变化,如有疑问可询问作者。
zero-knowledge protocol:是一组数学规则,根据这些规则,在给定 instance 后,prover 可以向 verifier 证明自己知道该 instance 的 witness 而不揭露 witness 任何信息。
设 $R$ 是域 $F_r$ 上的 R1CS,$R$ 的 Groth_16 参数如下:
$$ Groth\_16 - Param(R) = (r, G_1, G_2, e(·, ·), g_1, g_2) $$
$G_1, G_2$ 是有限循环群,阶为 $r$,$G_1$ 的生成器是 $g_1$,$G_2$ 的生成器是 $g_2$,$e: G_1 × G_2 → G_T$ 是对于 $G_T$ 的有效计算的、非退化的、双线性配对。这些参数通常需要预先协商。
Groth_16 协议如下:
- Setup 阶段 $(CRS, ST) ← S ETUP (R)$:SETUP 算法以 R1CS $R$ 作为输入,算出公共引用字符串 CRS(Common Reference String)和模拟后门 ST(simulation trapdoor)
- Prover 阶段 $π ← P ROVE (R,CRS, I,W )$:给定 $R$ 的 constructive proof $(I;W)$ ,算法 PROVE 将 $R$、$CRS$ 和 $(I;W)$ 作为输入,算出 zk-SNARK $π$
- Verify 阶段 $\left\{accept, reject\right\} ← V FY (R,CRS, I, π)$:算法将 $R$、$CRS$、instance $I$ 和 zk-SNARK $π$ 作为输入,输出 reject 或 accept
- $π ← S IM (R, τ, CRS, I)$:算法 SIM 将 $R$、后门 ST 的参数 $τ$、$CRS$、instance $I$ 作为输入,输出 zk-SNARK $π$
3-因子分解问题
QAP 定义于 $F_{13}$,所以必须选择阶为 13 的配对群 $G_1, G_2$
BLS6_6 有两个子群 $G_1[13], G_2[13]$,阶均为 13。相关的 Weil 配对 $e(·, ·)$ 是有效计算的、双线性、非退化的。所以可以选择这些群和 Weil 配对,$G_1[13],G_2[13]$ 的生成 器分别为 $g_1=(13,15),g_2=(7v^2,16v^3)$,得到如下参数:
$$ Groth-Param(R_{3.fac_zk}) = (13, G_1[13], G_2[13], e(·, ·), (13, 15), (7v^2 , 16v^3 ))) $$
参数的选择并非唯一,每对具有有效可计算、非退化双线性配对的 13 阶有限循环群都可以作为 Groth_16 参数集。
1 启动阶段
该阶段对于每个 R1CS 和关联的 QAP 只需执行一次,输出的 CRS 会被 prover 和 verifier 用于生成和验证 zk-SNARK。此外,还会生成一个模拟后门,可被用来模拟 proof。
设 $L$ 是 R1CS $R$ 定义的语言,该语言的一个 instance $<I_1, ..., I_n>$ 的一个 constructive proof 是 witness $<W_1, ..., W_m>$,$R$ 的 $QAP(R) = \left\{T ∈ F[x], \left\{ A_j, B_j, C_j ∈ F[x] \right\}_{h=0}^{n+m} \right\}$,$\left\{G_1, G_2, e(·, ·), g_1, g_2, F_r)\right\}$ 是 Groth_16 参数。
从标量域 $F_r$ 中随机选取 5 个可逆的元素 $α, β ,γ, δ, τ$,得到模拟后门(simulation trapdoor) ST:
$$ ST = (α, β ,γ, δ, τ) $$
这 5 个随机数和 2 个生成器 $g_1, g_2$ 以及 QAP 一起生成语言 $L$ 的公共引用字符串(Common Reference String)$ CRS_{QAP} = (CRS_{G_1}, CRS_{G_2})$:
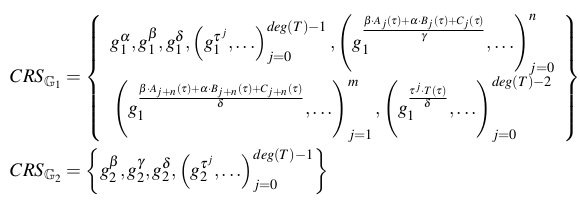
CRS 取决于后门,所以不是唯一的。CRS 大小与 instance 和 witness 的大小是线性相关的。
模拟后门 $ST = (α, β ,γ, δ, τ)$ 中的 $τ$ 为秘密评估点(secret evaluation point)。因为 $F_r$ 是有限循环群 $G_1, G_2$ 的标量域,所以 CRS 的一个关键特征是提供了一种在生成器 $g_1, g_2$ 的指数中计算度为 $deg(P) < dep(T)$ 的多项式 $P ∈ F_r [x]$,而不需要知道 $τ$。例如多项式 $P(x) = g_1^{a_0 · x^0 + a_1 · x^1 + . . . a_k · x^k}$,将 $τ$ 代入后,得到:
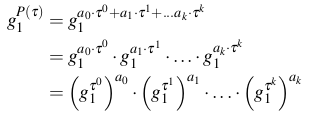
只需要知道 $τ$ 的幂(powers of tau) $g_{1 \space or \space 2}^{τ^j}$ 就可以算出 $g_1^{P(τ)}$,而 $g_{1 \space or \space 2}^{τ^j}$ 是 CRS 的一部分。同理可算出 $g_2^{P(τ)}$。
模拟后门被称为 toxic waste,因为可以生成欺诈 proof。CRS 也被称为 prover and verifier key pair。
模拟后门必须被丢弃,为此一般会引入多方计算,每方都持有后门的一部分,只要有一方不同意,后门就无法恢复。
2 证明阶段
给定 R1CS $R$ 和 instance $I=<I_1, ..., I_n>$,该阶段的目标是说服 verifier,prover 知道 $I$ 的 witness $W$,而不透露 $W$ 的任何知识。$(I;W)$ 是语言 $L_R$ 的一个单词。
为了构建一个 constructive proof,prover 需要计算 $W = <W_1, ..., W_m>$ 使得 $(<I_1, ..., I_n>;<W_1, ..., W_m>)$ 是 R1CS $R$ 的一个解。
生成 witness 后,prover 通过 QAP 计算多项式 $P_{(I;w)} = (A_0 + \sum_j^nI_jA_j + \sum_j^mW_jA_{n+j})(B_0 + \sum_j^nI_jB_j + \sum_j^mW_jB_{n+j}) - (C_0 + \sum_j^nI_jC_j + \sum_j^mW_jC_{n+j})$ ,然后使用 QAP 的目标多项式 $T$ 整除 $P_{(I;W)}$,得到 $H := P_{(I;W )} / T$。
然后在生成器 $g_1$ 的指数中计算秘密评估点 $τ$ 处的多项式 $(H · T )/δ$。设 $H(x) = P/T$:
$$ H(x) = H_0 · x^0 + H_1 · x^1 + . . . + H_k · x^k $$
为了在 $g_1$ 的指数中计算 $τ$ 处的 $(H · T )/δ$,prover 使用 CRS 计算如下:
$$ g_1^{\frac{H(τ) · T(τ)}{δ}} = (g_1^{\frac{τ^0 · T(τ)}{δ}})^{H_0} · (g_1^{\frac{τ^1 · T(τ)}{δ}})^{H_1} ... (g_1^{\frac{τ^k · T(τ)}{δ}})^{H_k} $$
然后随机选择两个域元素 $r,t ∈ F_r$,使用 $I_1, ...I_n$ 和 $W_1, ..., W_n$ 计算如下曲线点:
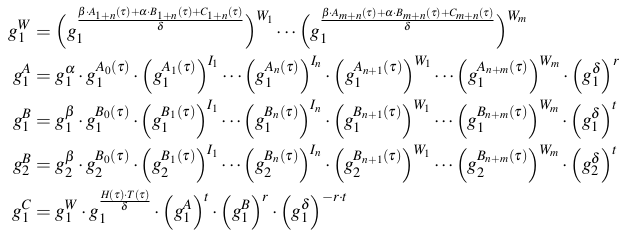
其中,群元素 $g_1^{A_j(τ)}, g_1^{B_j(τ)}, g_2^{B_j(τ)}$ 可从 CRS 和 QAP 获得,这些点只需要计算一次,且可被公开,可被重用,因为对于所有的 instance 和 witness 都是一致的。
便可得到一个合法的 Groth_16 的 zk-SNARK 参数 π:
$$ π = (g^A_1 , g^C_1 , g^B_2 ) $$
由 3 个曲线点组成,两个来自群 $G_1$,一个来自群 $G_2$。这种安排是有目的的,因为 $G_1$ 是素数域上的椭圆曲线的 torsion 群,$G_2$ 是扩展域上的 full torsion 群的子群。因为 $G_1$ 比 $G_2$ 所需的存储空间和计算更少,所以这种设计是较优的。
witness 编码到了安全曲线的生成器的指数中,这样就不会被暴露给任何人。此外,随机域元素 $r, t$ 使得每个 proof 随机化,确保不会有两个 proof 对应于同一个 witness。
3 验证阶段
给定 R1CS $R$、instance $I=<I_1, ..., I_n>$ 和 zk-SNARK $π$, $π$ 为有效 proof。如果后门已经不存在了,且 proof 通过来验证,那么 verifier 就可以确信存在一个 witness $W=<W_1, ..., W_m>$ 使得 $(I;W)$ 属于语言 $R$。
为了实现 Groth_16,假设 verifier 可以计算对映射 $e(·, ·)$,并可访问用于生成 $π$ 的 CRS。为了验证,verifier 计算如下曲线点:
$$ g_1^I=(g_1^{\frac{β·A_0(τ)+α·B_0 (τ)+C_0 (τ)}{γ}}) · (g_1^{\frac{β·A_1(τ)+α·B_1(τ)+C_1(τ)} {γ}})^{I_1} ··· (g_1^{\frac{β·A_n(τ)+α·B_n(τ)+C_n(τ)}{γ}})^{I_n} $$
有了这些群元素,verifier 就可以使用配对映射通过如下等式验证 zk-SNARK $π = (g^A_1 , g^C_1 , g^B_2 )$:
$$ e(g^A_1 , g^B_2 ) = e(g^α_1 , g_2^β ) · e(g^I_1 , g_2^γ ) · e(g^C_1 , g^δ_2 ) $$
如果等式成立,则 verifier 输出 accept;否则,输出 reject。
配对 $e(g^α_1 , g_2^β )$ 独立于 proof,所以只需计算一次,然后成为 verifier key 的一部分。
4 模拟 proof 阶段
在启动阶段,创建了 CRS 和一个模拟后门,该后面应该在启动阶段结束后被丢弃。有了该后门,可以在不知道 witness 的情况下生成 zk-SNARK。
假设攻击者可以访问 Groth_16 参数,QAP,CRS 和相应的后门 ST:
$$ ST = (α, β ,γ, δ, τ) $$
给定 instance $I$,欺诈者可以生成该 instance 的 zk-SNARK,并可通过验证,而不需要知道该 instance 的witness $W$。
欺诈者可以使用模拟后门、QAP、任意两个来自配对群的标量域 $F_r$ 的域元素 $A, B$ 来计算给定 instance $<I_1, ..., I_n>$ 的 $g_1^C$:
$$ g_1^C = g_1^{\frac{A·B}{δ}} · g_1^{-\frac{α·β}{δ}} · g_1^{-\frac{β A_0 (τ)+αB_0 (τ)+C_0 (τ)}{δ}} · (g_1^{-\frac{β A_1 (τ)+αB_1 (τ)+C_1 (τ)}{δ}})^{I_1} ··· (g_1^{-\frac{β A_n(τ)+αB_n(τ)+C_n(τ)}{δ}})^{I_n} $$
其中,$g_1, g_2$ 是已知的,因为已经作为 $g_1^{τ^0}, g_2^{τ^0}$ 而被包含在了 CRS 中,所以欺诈者可以算出 $g_1^{A·B}$。另外,模拟后门中的每个参数都是已知的,所以可以算出 $g_1^C$ 中的剩余部分。
然后发布 zk-SNARK $π_{forged} = (g^A_1 , g^C_1 , g^B_2 )$,可以通过验证,并且在不知道 $<W_1, ..., W_m>$ 的情况下是可计算的。
# 参考
The MoonMath Manual 第 8 章


没有评论