这篇文章上次修改于 240 天前，可能其部分内容已经发生变化，如有疑问可询问作者。

1 形式语言

形式语言给出：语句的形式 proof 是什么。

设 $\sum$ 是任意集合，$\sum^*$ 是所有的长度有限的字符串 $<x_1, .., x_n>$，其中 $x_j$ 取自 $\sum$，空字符串 $<> ∈ \sum^* $。语言 L 是 $\sum^*$ 的子集。在这种情况下，$\sum$ 是语言 L 的子母表，$\sum$ 中的元素是字母，L 中的元素是单词。如果有规则指定 $\sum^*$ 中的字符串是否属于语言，该规则就被称为语法。如果 $L_1$ 和 $L_2$ 是基于同一个字母表的两个形式语言，且包含了相同的单词集，则称 $L_1$ 和 $L_2$ 是等价的。

1.1 Decision functions

在 SNARK 开发中，语言通常被定义为决策问题（decision problems），决策关系（deciding relation）$R ⊂ \sum^*$ 决定了字符串 $x ∈ \sum^∗$ 是否是语言中的单词。如果 $x ∈ R$，那么 $x$ 是语言 $L_R$ 中的单词，否则不是。关系 $R$ 总结了语言 $L_R$ 的语法，也称为决策函数（decision function）：

$$ R: \sum^* \rightarrow \left\{true, \space, false \right\} $$

可用 R 定义语言：

$$ L_R := \left\{x ∈ \sum^∗ \space | \space R(x) = true \right\} $$

语句（statement）S 是语言 L 包含单词 x 的声明，即存在一些 $x ∈ L$。语句 S 的构造性证明（constructive proof）是给定一些字符串 $P ∈ \sum^* $ 并且该证明是通过 $R(P) = true$ 而被验证的（verified）。这种情况下，P 被称为语句 S 的一个实例（instance）。

3-因子分解例子

设 $\sum := F_{13}$，$L_{3.fac}$ 包含由来自 $F_{13}$ 的 4 个元素组成的字符串 $<x_1, x_2, x_3, x_4>$，且满足 $x_1 · x_2 · x_3 = x_4$。例如 <2, 12, 4, 5> 是 $L_{3.fac}$ 中的单词，而 <2, 12, 11> 就不是。可通过决策函数来更加形式化地描述 $L_{3.fac}$ ：

$$ R_{3.fac}: (F_{13}^*) × (F_{13}^*) \rightarrow \left\{true, false \right\}; \space <x_1, ..., x_n> \rightarrow \begin{cases} true & n = 4 \space and \space x_1 · x_2 · x_3 = x_4 \\ false & else\space \end{cases} $$

字符串 <2, 12, 4, 5> 就是 $L_{3.fac}$ 包含单词的 constructive proof，$R_{3.fac}(<2, 12, 4, 5>) = true$ 是证明的验证。

1.2 Instance and Witness

语句在形式化语言中提供了成员关系声明，而实例则是这些声明的 constructive proof。在零知识证明系统中，可以隐藏 proof instance 的一部分，但仍然能证明语句。因此，在这种情况下，需要将 proof 分为未隐藏的公共部分（称为 instance）和隐藏的私有部分（称为 witness）。

为了将 proof instance 分为 instance 和 witness，前面的形式语言定义需要做些调整。不再使用单个子母表，而是使用两个子母表 $\sum_I$ 和 $\sum_W$，决策函数定义如下：

$$ R: {\sum}_I^* × {\sum}_W^* \rightarrow \left\{true, false \right\}; (i; w) \rightarrow R(i; w) $$

字符串 $(i; w) ∈ {\sum}_I^* × {\sum}_I^* $，$R(i; w) = true$。输入 i 为 instance，输入 w 为 witness。

语言的定义如下：

$$ L_R : = \left\{ {\sum}_I^* × {\sum}_I^* \space | \space R(i; w) = true\right\} $$

语句 S 是声明：给定 instance $i ∈ {\sum}_I^* $，总存在 witness $w ∈ {\sum}_I^* $ 使得语言 L 包含单词 (i; w)。语句 S 的一个 constructive proof 是存在字符串 $P (i; w) ∈ {\sum}_I^* × {\sum}_I^*$，且 proof 被 $R(P) = true$ 验证（verified）。

证明系统需要在不暴露 witness 的情况下证明语句。

语句可以被视为知识声明，而证明者声称知道对于给定 instance 的 witness。

3-因子分解例子：$x_1, x_2, x_3$ 是 witness，乘积 $x_4$ 是 instance。$L_{3.fac}$ 重新定义如下：

$$ R_{3.fac\_zk}: (F_{13}^*) × (F_{13}^*) \rightarrow \left\{true, false \right\}; (<i_1, ..., i_n>, <w_1, ..., w_m>)\rightarrow \begin{cases} true & n = 1, m=3, i_1 = w_1 · w_2 · w_3 \\ false & else\space \end{cases} $$

也可以选择 $x_4$ 为 witness，$x_1, x_2, x_3$ 为 instance，或者都选为 witness，或者都选为 instance，取决于应用。

语言 $L_{3.fac\_zk}$ 就是使得决策函数 $R_{3.fac\_zk}$ 为 true 的选自 $(F_{13}^*) × (F_{13}^*)$ 的字符串集合。

1.3 模块化

开发者通常需要使用简单的语句来构造复杂的语句。在零知识证明系统中，那些简单的块通常被称为小装置（gadgets），gadgets 库会包含原子类型如 bool、整型和一些哈希函数，椭圆曲线等。为了合成语句，开发者需要将预定义好的 gadgets 合成复杂的逻辑，称这种能力为模块化（modularity）。

2 语句表示

2.1 Rank-1 Quadratic Constraint Systems

尽管决策函数可以用各种方式表达，但是许多现代证明系统要求决策函数使用有限域上的二次方程组来表示。

秩-1 (二次 ) 约束系统（R1CS，Rank-1 (quadratic) Constraint Systems ）是零知识证明系统中的常见标准。

2.1.1 R1CS 表示

先将每个式子写成 $a \cdot b = c$ 的形式。

例如对于 $y=x^2 + 1$，先展开，得到

$$ \begin{align} & v = x \cdot x \\ & out = v + 1\\ \end{align} $$

所有的变量表示为 $S=[1, x, out, v]$，然后每个式子可重新用 $(a \cdot S) \cdot (b \cdot S) = (c \cdot S)$ 的形式表示。

对于第 1 个式子，$a=[0, 1, 0, 0], b=[0, 1, 0, 0], c=[0, 0, 0, 1]$

对于第 2 个式子，$a=[1, 0, 0, 1], b=[1, 0, 0, 0], c=[0, 0, 1, 0]$，其中，$a$ 是 $v+1$ 的结果

从而得到

$$ A=\begin{pmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 \\ \end{pmatrix}, B=\begin{pmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \end{pmatrix}, C=\begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} $$

形式化表示

设 F 是域，$n, m, k ∈ $ N，$a_j^i, b_j^i, c_j^i ∈$ F，其中 $0 \le j \le n + m$ 且 $1 \le i \le k$，R1CS 可用如下 k 个等式表示：

$$ (a_0^1 + \sum_{j=1}^na_j^1·I_j + \sum_{j=1}^ma_{n+j}^1·W_j)·(b_0^1 + \sum_{j=1}^nb_j^1·I_j + \sum_{j=1}^mb_{n+j}^1·W_j) = c_0^1 + \sum_{j=1}^nc_j^1·I_j + \sum_{j=1}^m·c_{n+j}^1·W_j\\ $$

$$ ... \\ $$

$$ (a_0^k + \sum_{j=1}^na_j^k·I_j + \sum_{j=1}^ma_{n+j}^k·W_j)·(b_0^k + \sum_{j=1}^nb_j^k·I_j + \sum_{j=1}^mb_{n+j}^k·W_j) = c_0^k + \sum_{j=1}^nc_j^k·I_j + \sum_{j=1}^m·c_{n+j}^k·W_j\\ $$

k 为约束的个数，每个等式被称为约束。满足所有约束的 $<I_1, .., I_n>;<W_1, ..., W_m>$ 中，$<I_1, .., I_n>$ 为 instance，$<W_1, .., W_m>$ 为 witness。

R1CS 的解就是程序正确执行的 proof。

3-因子分解例子

$F_{3.fac\_zk}$ 中包含取自 $F_{13}$ 中的单词 $(<I_1>;<W_1,W_2,W_3>)$，且 $I_1 = W_1 · W_2 · W_3$。将将其重写为 R1CS 如下：

为了避免 3 个数相乘，引入 $W_4$

$$ W_1·W_2 = W_4 \\ $$

$$ W_4·W_3 = I_1 $$

也可以写成：

$$ W_2·W_3 = W_4 \\ $$

$$ W_4·W_1 = I_1 $$

R1CS 不是唯一的。

选择 n = 1, m = 4, k = 2，得到如下值：

$$ \begin{matrix} a_0^1=0 & a_1^1=0 & a_2^1=1 & a_3^1=0 & a_4^1=0 & a_5^1=0 \\ a_0^2=0 & a_1^2=0 & a_2^2=0 & a_3^2=0 & a_4^2=0 & a_5^2=1 \\ b_0^1=0 & b_1^1=0 & b_2^1=0 & b_3^1=1 & b_4^1=0 & b_5^1=0 \\ b_0^2=0 & b_1^2=0 & b_2^2=0 & b_3^2=0 & b_4^2=1 & b_5^2=0 \\ c_0^1=0 & c_1^1=0 & c_2^1=0 & c_3^1=0 & c_4^1=0 & c_5^1=1 \\ c_0^2=0 & c_1^2=1 & c_2^2=0 & c_3^2=0 & c_4^2=0 & c_5^2=0 \\ \end{matrix} $$

然后可重写为：

$$ (a_0^1 + a_1^1I_1 + a_2^1W_1 + a_3^1W_2 + a_4^1W_3 + a_5^1W_4) · (b_0^1 + b_1^1I_1 + b_2^1W_1 + b_3^1W_2 + b_4^1W_3 + b_5^1W_4) \\ = (c_0^1 + c_1^1I_1 + c_2^1W_1 + c_3^1W_2 + c_4^1W_3 + c_5^1W_4) \\ $$

$$ (a_0^2 + a_1^2I_1 + a_2^2W_1 + a_3^2W_2 + a_4^2W_3 + a_5^2W_4) · (b_0^2 + b_1^2I_1 + b_2^2W_1 + b_3^2W_2 + b_4^2W_3 + b_5^2W_4) \\ = (c_0^2 + c_1^2I_1 + c_2^2W_1 + c_3^2W_2 + c_4^2W_3 + c_5^2W_4) \\ $$

即

$$ A=\begin{pmatrix} 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{pmatrix}, B=\begin{pmatrix} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix}, C=\begin{pmatrix} 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 0 \\ \end{pmatrix} $$

2.1.2 R1CS 可满足性

R1CS 定义了形式语言，每个域 F 上的 R1CS 都定义了基于子母表 $\sum_I × \sum_W = F × F$ 的决策函数：

$$ R_{R1CS}: (F)^* × (F)^* \rightarrow \left\{true, false \right\} \rightarrow \begin{cases} true & (I;W) \space satisfies \space R1CS \\ false & else \end{cases} $$

语句是知识声明：给定 instance I，存在 witness W 使得 (I; W) 是 R1CS 的解。

$\sum = F$，语言定义如下：

$$ L_{R1CS\_SAT(F)} = \left\{(i; w) ∈ {\sum}^* × {\sum}^* \space | \space there \space is \space a \space R1CS \space R \space such \space that \space R(i;w) = true \right\} $$

3-因子分解例子：对于 $I_1 = 11$，为了证明语句“存在 witness W 使得 $(I_1; W)$ 属于 $L_{3.fac\_zk}$”，一个 proof 必须是 R1CS 的解，即提供一组 witness 变量 $W_1, W_2, W_3, W_4$ 的赋值。一个正确的 constructive proof 是 $π =< 2, 3, 4, 6 >$

2.2 代数电路

2.2.1 代数电路表示

设 F 是域，一个代数电路 C(F) 是可以在 F 上计算一个多项式的有向无环（多重）图。源点代表函数的变量和常量，终点代表函数的输出。所有的节点都仅有两条入边，代表着域上的加法或乘法运算。边的方向代表沿着节点的计算流。

既不是源点也不是终点的节点称为算术门（arithmetic gates）。被 + 标记的算术门称为加法门（addition-gates），被 · 标记的称为乘法门（multiplication-gates）。每个算术门都恰好有两个输入，用两条入边表示。

因为边是有序的，所以可以写为 $<E_1, E_2, ..., E_n>$，$n ∈$ N。边的标签可以说常量或符号如 $I_j, W_j$，分别表示 instance 变量和 witness 变量。在绘制电路的最初的阶段，在没有确定一条边是 $I$ 还是 $W$ 时，可以先用 $S_j$ 标签。

3-因子分解例子

$f_{3.fac}: F_{13} × F_{13} × F_{13} \rightarrow F_{13};(x_1, x_2, x_3) \rightarrow x_1 · x_2 · x_3$。一个合理的 witness 是 $f_{3.fac}$ 在点 $I_1 ∈ F_{13}$ 处的原像，即 $f_{3.fac}(W_1, W_2, W_3) = I_1$

要将该函数转为 $F_{13}$ 上的代数电路，要先在函数的定义中引入括号，改写为二元运算：

$$ \begin{align} f_{3.fac}(x_1, x_2, x_3) & = x_1 · x_2 · x_3 \\ & = (x_1 · x_2) · x_3 \\ & = MUL(MUL(x_1, x_2), x_3) \\ \end{align} $$

边的标签为 $W_1 = x_1, W_2 = x_2, W_3 = x_3, I_1 = f_{3.fac}(x_1, x_2, x_3)$，得到如下电路：

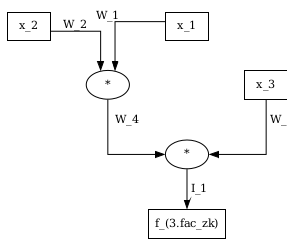
该图有 3 个叶子节点 $x_1, x_2, x_3$，1 个根节点 $f_{3.fac(x_1, x_2, x_3)}$ 和 2 个中间节点，均为乘法门。

电路不是唯一的，取决于括号的顺序。

2.2.2 电路执行

电路执行：根据输入获得输出。值从一个节点沿着边到达另一个节点，如果节点是门，则值会被转换，重复整个过程直到到达终点。

电路的正确执行中，不仅会获得输出，还会获得边上的值，将获得的边集值 $<S_1, S_2, ..S_n>$ 称为电路的合法赋值（valid assignment），该合法赋值也被称为电路正确执行的证明（proofs for proper circuit execution）

3-因子分解例子

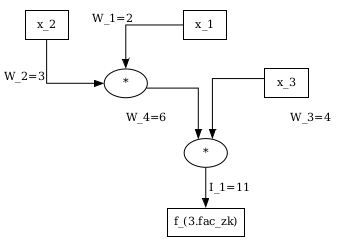
边集为 $S := <I_1; W_1, W_2, W_3, W_4>$，一个合法赋值是 $S_{valid} := <11; 2, 3, 4, 6>$

2.2.3 电路可满足性

为了理解电路是如何产生形式语言，可以看到每个域 F 上的代数电路 C(F) 都定义了一个基于字母表 $\sum_I × \sum_W $ 的决策函数：

$$ R_{C(F)}: F^* × F^* \rightarrow \left\{true, false \right\};(I;W) \rightarrow \begin{cases} true & (I;W) \space is \space a \space valid \space assignment \space to \space C(F) \\ false & else \end{cases} $$

语法是电路的形状，单词是电路正确执行时边的赋值，语句是声称知道“给定 instance I，存在 witness W 使得 (I; W) 是电路的合法赋值”。语句的一个 constructive proof 是为每个 witness 变量分配一个域元素，且该分配通过了电路执行的验证。

在零知识证明系统中，电路的执行通常被称为 witness generation，因为 instance 通常是公开的，所以任务就是计算 witness。

满足电路的语言：

$$ L_{CIRCUIT\_SAT(F)} = \left\{(i;w) ∈ {\sum}^* ∈ {\sum}^* \space | \space there \space is \space a \space circuit \space C(F) \space such \space that \space (i; w) \space is \space valid \space assignment \right\} $$

2.2.4 关联约束系统

本节讲述如何将电路转为 R1CS。

C(F) 是有限域 F 上的代数电路，边的标签组成的字符串为 $<S_1, S_2, .., S_n>$。从一个空的 R1CS 开始，每条边 $S_j$ 上都执行如下其中一个步骤：

如果边 $S_j$ 是乘法门的出边，则 R1CS 得到一个新的约束：(left input) · (right input) = $S_j$
如果边 $S_j$ 是加法门的出边，则 R1CS 得到一个新的约束：(left input + right input) · 1 = $S_j$
没有其它边可以为系统添加一个约束。

每个代数电路 C(F) 都可以生成一个 RICS $R$，称为该电路的关联 R1CS。

3-因子分解例子

将如下电路转为 R1CS。

为了生成所有约束，需要迭代边标签集 $<I_1; W_1, W_2, W_3, W_4>$：

从 $I_1$ 开始，是一条乘法门的出边，入边都有标签，所以得到约束：$W_4 · W_3 = I_1$
然后考虑 $W_1$，因为不是乘法门或加法门的出边，所以不会添加约束。$W_2$ 同理。
对于 $W_4$，是乘法门的出边，入边都有标签，所以得到约束：$W_2 · W_1 = W_4$
因为没有更多有标签的边了，所以所有的约束都生成了，把它们合在一起，生成了 $C_{3.fac}(F_{13})$的关联 R1CS：
$$ W_4 · W_3 = I_1 \\ W_2 · W_1 = W_4 $$

2.3 Quadratic Arithmetic Programs

R1CS 可转为 Quadratic Arithmetic Program [QAP]，QAP 是目前存在的一些最有效的 ZK-SNARK proof 生成器的基础。

2.3.1 QAP 表示

回顾之前的 R1CS：

$$ A=\begin{pmatrix} 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ \end{pmatrix}, B=\begin{pmatrix} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix}, C=\begin{pmatrix} 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 0 \\ \end{pmatrix} $$

将 R1CS 中的 $A, B, C$ 三个矩阵中的每列转换为多项式。例如对于矩阵 $A$，第一列元素是 $[0, 0]$，将每个元素作为 y 坐标，下标为 x 坐标，就可以得到两个点 (0, 0), (1, 0)，从而得到一个 1 度多项式。所以矩阵 $A$ 会算出 5 个多项式，矩阵 $B, C$ 同理。

形式化表示

设 F 是域，$R$ 是 F 上的一个 R1CS，F 中的非 0 元素个数大于$R$ 中的约束个数 $k$。$a_j^i, b_j^i, c_j^i ∈$ F 定义 R1CS 的常数，其中 $0 ≤ j ≤ n + m, \space 1 ≤ i ≤ k$，$m_1, ..., m_k$ 是 F 中的任意可逆的不同的元素。R1CS 的一个 Quadratic Arithmetic Program 是 F 上的如下多项式集合：

$$ QAP(R) = \left\{T ∈ F[x], \left\{ A_j, B_j, C_j ∈ F[x] \right\}_{h=0}^{n+m} \right\} $$

$T(x) := \prod_{l=1}^k(x-m_l)$ 是度为 k 的多项式，称为 QAP 的目标多项式，$A_j, B_j, C_j$ 均是度为 k - 1 的多项式，定义如下：

$$ A_j(m_i) = a_j^i, \space B_j(m_i)=b_j^i, \space C_j(m_i) = c_j^i \space for \space all \space j=1, ..., n+m+1, i=1, ...k $$

给定 R1CS，一个关联的 QAP 可通过如下步骤算出：

如果 R1CS 包含 k 个约束，则先从 F 中选取 k 个不同的可逆元素，每种选择都会生成不同的 QAP。
计算目标多项式 T。
对于每个 $1 \le j \le k$，使用如下点集根据 Lagrange 插值法计算多项式 $A_j$
$$ S_{A_j} = \left\{(m_1, a_j^1), ..., (m_k, a_j^k) \right\} $$
同理，对于每个 $1 \le j \le k$ 计算 $B_j,\space C_j$

3-因子分解例子

R1CS 如下

$$ W_1 ·W_2 = W_4 \\ W_4 ·W_3 = I_1 $$

R1CS 中的常量 $a_j^i, b_j^i, c_j^i$ 如下

即

因为 R1CS 定义于 $F_{13}$ 上，有 2 个约束，所以需要从 $F_{13}$ 中选择两个任意可逆的元素 $m_1, m_2$，我们选择 $m_1=5, m_2=7$，得到目标多项式：

$$ \begin{align} T(x) &= (x-m_1)(x-m_2) \\ &= (x-5)(x-7) \\ &= (x+8)(x+6) \\ &= x^2 + x + 9 \\ \end{align} $$

然后根据 R1CS 的系数计算多项式 $A_j, B_j, C_j$。因为 R1CS 有两个约束等式，所以 $A_j, B_j, C_j$ 的度为 k - 1 = 1，且被点 $m_1=5$ 和 $m_2=7$ 处的等式定义。

在点 $m_1$，每个多项式 $A_j$ 都被定义为 $a_j^1$；在点 $m_2$，每个多项式 $A_j$ 都被定义为 $a_j^2$，$B_j, C_j$ 同理，得到：

$$ \begin{matrix} A_0(5)=0 & A_1(5)=0 & A_2(5)=1 & A_3(5)=0 & A_4(5)=0 & A_5(5)=0 \\ A_0(7)=0 & A_1(7)=0 & A_2(7)=0 & A_3(7)=0 & A_4(7)=0 & A_5(7)=1 \\ B_0(5)=0 & B_1(5)=0 & B_2(5)=0 & B_3(5)=1 & B_4(5)=0 & B_5(5)=0 \\ B_0(7)=0 & B_1(7)=0 & B_2(7)=0 & B_3(7)=0 & B_4(7)=1 & B_5(7)=0 \\ C_0(5)=0 & C_1(5)=0 & C_2(5)=0 & C_3(5)=0 & C_4(5)=0 & C_5(5)=1 \\ C_0(7)=0 & C_1(7)=1 & C_2(7)=0 & C_3(7)=0 & C_4(7)=0 & C_5(7)=0 \\ \end{matrix} $$

使用 $S_{A_2} = \left\{(m_1, a_2^1), (m_2, a_2^2)\right\} = \left\{(5, 1), (7, 0)\right\}$ 借助 Lagrange 插值法计算 $A_2$：

$$ \begin{align} A_2(x) & = a_2^1(\frac{x-m_2}{m_1-m_2}) + a_2^2(\frac{x-m_1}{m_2-m_1}) \\ & = 1 · (\frac{x-7}{5-7}) + 0 · (\frac{x-5}{7-5}) \\ & = \frac{x-7}{-2} = \frac{x-7}{11} \\ & = 6(x-7) = 6x + 10 \end{align} $$

同理可算出其它多项式。最终得到：

$$ QAP(R_{3.fac\_zk}) = \left\{x^2+x+9, \left\{0, 0, 6x+10, 0, 0, 7x+4\right\}, \left\{0, 0, 0, 6x+10, 7x+4, 0\right\}, \left\{0, 7x+4, 0, 0, 0, 6x+10\right\} \right\} $$

2.3.2 QAP 可满足性

设 $R$ 是 R1CS，相关的变量为 $(<I_1, ..., I_n>;<W_1, ..., W_m)$，QAP 为 $R$ 的一个 Quadratic Arithmetic Program，当如下多项式可被目标多项式 $T$ 整除时，$(<I_1, ..., I_n>;<W_1, ..., W_m)$ 是 R1CS 的解：

$$ P_{(I;w)} = (A_0 + \sum_j^nI_jA_j + \sum_j^mW_jA_{n+j})(B_0 + \sum_j^nI_jB_j + \sum_j^mW_jB_{n+j}) - (C_0 + \sum_j^nI_jC_j + \sum_j^mW_jC_{n+j}) $$

域 F 上的 QAP 基于字母表 $\sum_I × \sum_W = F × F$ 定义了一个决策函数：

$$ R_{QAP}: (F)^* × (F)^* \rightarrow \left\{true, false \right\}; (I;W) \rightarrow \begin{cases} true & P_{(I;W)} \space is \space divisible \space by \space T \\ false & else \end{cases} $$

在 QAP 中，一个合法的 proof 是包含一个可被 $T$ 整除的多项式 $P_{(I;W)}$。

给定 instance $I$，为了计算 $L_{QAP}$ 中一个语句的 constructive proof，证明者需要计算关联 R1CS 的一个 constructive proof $W$，例如运行 R1CS 的电路。有了 $(I;W)$，证明者就可以计算多项式 $P_(I;W)$，并将该多项式公布为 proof。

3-因子分解例子

给定 $I_1 = 11$，我们知道 $(W_1, W_2, W_3, W_4) = (2, 3, 4, 6)$ 是一个正确的 witness，因为 $(<I_1>;<W_1, W_2, W_3, W_4>) = (<11>;<2, 3, 4, 6>)$ 是电路的一个合法赋值，所以是 $R_{3._fac\_zk}$ 的解，是语言 $L_{R_{3.fac\_zk}}$ 的 constructive proof。

为了将 constructive proof 转为语言 $L_{R_{3.fac\_zk}}$ 的指数证明，证明者需要使用 constructive proof 中的元素计算多项式 $P_{(I;W)}$：

$$ \begin{align} P_{(I;W)} &= (A_0 + \sum_j^nI_jA_j + \sum_j^mW_jA_{n+j})(B_0 + \sum_j^nI_jB_j + \sum_j^mW_jB_{n+j}) - (C_0 + \sum_j^nI_jC_j + \sum_j^mW_jC_{n+j}) \\ &= (2(6x+10) + 6(6x+4))· (3(6x + 10) + 4(7x + 4)) − (11(7x + 4) + 6(6x + 10)) \\ &=((12x + 7) + (3x + 11)) · ((5x + 4) + (2x + 3)) − ((12x + 5) + (10x + 8)) \\ &=(2x + 5) · (7x + 7) − (9x) \\ &=(x^2 + 2 · 7x + 5 · 7x + 5 · 7) − (9x) \\ &=(x^2 + x + 9x + 9) − (9x) \\ &=x^2 + x + 9 \\ \end{align} $$

因为 $P_{(I;W)}$ 等于目标多项式 $T$，所以可被其整除 $P / T = 1$，所以验证者验证了该 proof 是对的。

3 Circom

编译为 R1CS 的编程语言在密码学和区块链中比较流行，这些语言提供了设计和实现代数电路的更高级抽像。有了这些编程语言，开发者只需要专注于电路逻辑，编译器会负责输出 R1CS 和其它用于有效计算电路赋值的程序。

Circom 是设计代数电路的领域专用语言。它将电路编译为 R1CS，并输出 WebAssembly 和 C++ 程序。

Circom 中的概念：

信号（signal）是底层域 F 的一个元素，是不可更改的，可定义为输入或输出。输入信号是私有的，除非特意声明为公有，而输出信号是公有的。剩余的信号是私有的，且不可被声明为公有。
模板（template）是创建通用电路的算法。模板是一个新的电路对象，可被其它电路使用。
组件（component）定义了代数电路，有输入信号，输出信号和中间信号，和常量集合。与信号一样，是不可变的。

如下是一个 Circom 程序示例 trivial_circuit.circom：

template trivial_circuit() {
    signal private input in1 ;
    signal private input in2 ;
    var outc1 = 0 ;
    var inc1 = 7 ;
    signal output out1 ;
    signal output out2 ;
    out2 <== in1 ;
    outc1 === in2 ;
}
component main = trivial_circuit() ;

需注意，Circom 没有明确表示底层域，所以常量 0 和 7 没有直接意义。

使用如下命令进行编译：

circom trivial_circuit.circom --r1cs --wasm --sym

Circom 编译器会生成 3 个文件

trivial_circuit.r1cs 包含 R1CS，是二进制形式
trivial_circuit.wasm 是 wasm 代码可以根据给定 instance 计算 witness，是 R1CS 的解
trivial_circuit.sym 是符号文件，用于 debug 或打印 R1CS

3-因子分解的例子（$x_4 = x_1 · x_2 · x_3$）

template Multiplier() {
    signal input a ;
    signal input b ;
    signal output c ;
    c <== a*b ;
}
template three_fac () {
    signal input x1 ;
    signal input x2 ;
    signal input x3 ;
    signal output x4 ;
    component mult1 = Multiplier() ;
    component mult2 = Multiplier() ;
    mult1.a <== x1 ;
    mult1.b <== x2 ;
    mult2.a <== mult1.c ;
    mult2.b <== x3 ;
    x4 <== mult2.c ;
}
component main = three_fac() ;

编译：

circom three_fac.circom --r1cs --wasm --sym

打印电路状态，包括约束个数：

snarkjs r1cs info circuit.r1cs
[INFO] snarkJS: Curve: bn-128
[INFO] snarkJS: # of Wires: 6
[INFO] snarkJS: # of Constraints: 2
[INFO] snarkJS: # of Private Inputs: 0
[INFO] snarkJS: # of Public Inputs: 3
[INFO] snarkJS: # of Labels: 11
[INFO] snarkJS: # of Outputs: 1

参考

The MoonMath Manual 第 6 章
zkSNARKs: R1CS and QAP

阿萍的博客

密码学[4]：电路 R1CS QAP

1 形式语言

1.1 Decision functions

1.2 Instance and Witness

1.3 模块化

2 语句表示

2.1 Rank-1 Quadratic Constraint Systems

2.1.1 R1CS 表示

形式化表示

2.1.2 R1CS 可满足性

2.2 代数电路

2.2.1 代数电路表示

2.2.2 电路执行

2.2.3 电路可满足性

2.2.4 关联约束系统

2.3 Quadratic Arithmetic Programs

2.3.1 QAP 表示

形式化表示

2.3.2 QAP 可满足性

3 Circom

参考

没有评论