这篇文章上次修改于 807 天前,可能其部分内容已经发生变化,如有疑问可询问作者。
1 整数
整数:没有小数的数字,用 Z 表示。
自然数:所有的正整数,用 N 表示。
实数:可用 n/m 表示,n ∈ Z,m ∈ N,用 Q 表示。
素数:对于自然数 p ∈ N,只可被自身和 1 整除,用 P 表示。
自然数的素数分解:每个自然数 n 都可分解为一系列素数,n = p1 · p2 · ... · pk
欧几里得除法:对于两个整数 a ∈ Z 和 b ∈ Z,且 b != 0,总是存在一个整数 m ∈ Z 和一个自然数 r ∈ N,0 ≤ r < |b|,使得 a = m · b + r,a 为被除数,b 为除数,m 是商,r 是余数。例如,−17 = −5 · 4 + 3
扩展的欧几里得算法:在计算两个自然数 a, b ∈ N 最大公约数(greatest common divisor)的同时,还能找到两个整数 s, t ∈ Z,使得 gcd(a, b) = s · a + t · b 成立。
扩展的欧几里得算法实现:
pub fn extended_euclidean(a: i32, b: i32) -> (i32, i32, i32) {
if b == 0 {
return (a, 1, 0);
}
let (d, mut t, s) = ext_euclidean(b, a % b);
t -= a / b * s;
return (d, s, t);
}
#[cfg(test)]
mod tests {
use super::ext_euclidean;
#[test]
fn test_ext_euc() {
let a = 6;
let b = 8;
let (d, s, t) = extended_euclidean(a, b);
// [output] d: 2, s: -1, t: 1
println!("d: {}, s: {}, t: {}", d, s, t);
assert_eq!(a % d, 0);
assert_eq!(b % d, 0);
assert_eq!(d, s * a + t * b);
}
}两个整数互质:gcd(a, b) = 1
整数的表示:10 进制,2 进制(加上前缀 0b)、8 进制(加上前缀 0o)、16 进制(加上前缀 0x)
2 模
相似:两个整数 a, b ∈ Z 模一个自然数 n ∈ N, n >= 2 后相等,即 a mod n = b mod n,也可写作 a ≡ b ( mod n )
计算规则:
- 平移性:a1 ≡ b1 ( mod n ) ⇔ a1 + k ≡ b1 + k ( mod n )
- 缩放性:a1 ≡ b1 ( mod n ) ⇒ k · a1 ≡ k · b1 ( mod n )
- gcd(k, n) = 1 and k · a1 ≡ k · b1 ( mod n ) ⇒ a1 ≡ b1 ( mod n )
- k · a1 ≡ k · b1 ( mod k · n ) ⇒ a1 ≡ b1 ( mod n )
- 兼容加法:a1 ≡ b1 ( mod n ) 且 a2 ≡ b2 ( mod n ) ⇒ a1 + a2 ≡ b1 + b2 ( mod n )
- 兼容乘法:a1 ≡ b1 ( mod n ) 且 a2 ≡ b2 ( mod n ) ⇒ a1 ·a2 ≡ b1 ·b2 ( mod n )
费马小定理(Fermat's little theorem):对于素数 p ∈ P 和整数 k ∈ Z, 有 k^p ≡ k ( mod p )。
所以,如果 k 和 p 互质,两边可同时除以 k,可得到 k^(p-1) ≡ 1 ( mod p )
中国余数定理(Chinese Remainder Theorem):对于 k ∈ N 个互质的自然数 n1, n2, ..., nk ∈ N,以及任意的整数 a1, a2, ..., ak ∈ Z,下列一元线性同余方程组有解,且方程组任意两个解 x1, x2 模 N 同余,其中 N = n1 ·...· nk,即解的集合为 { x + m · N | m ∈ Z }
x ≡ a1 ( mod n1 )
x ≡ a2 ( mod n2 )
...
x ≡ ak ( mod nk )中国余数定理实现:
pub fn chinese_remainder(n: Vec<i32>, a: Vec<i32>) -> (i32, i32) {
assert_eq!(n.len(), a.len());
let mut n_product = 1;
for i in n.iter() {
n_product *= *i;
}
let it = n.into_iter().zip(a.into_iter());
let mut x = 0;
for (ni, ai) in it {
let nn = n_product / ni;
let (_, s, _) = extended_euclidean(nn, ni);
x += ai * s * nn;
x %= n_product;
}
(x, n_product)
}
#[cfg(test)]
mod tests {
use super::*;
#[test]
fn test_chinese_remainder() {
let n: Vec<i32> = vec![7, 3, 5, 11];
let a: Vec<i32> = vec![4, 1, 3, 0];
let (x, n_product) = chinese_remainder(n, a);
assert_eq!(x, 88);
assert_eq!(n_product, 1155);
}
}余数类(remainder class or residue class):模 n 后余数相等的一类数字。
余数类上的运算:假如 n = 6,2 + 5 = 8 + 11,因为 2 ≡ 8 ( mod 6 ),5 ≡ 11 ( mod 6 )
$Z_6$ 表示余数为 6 的余数类及相关的运算。
模逆 Modular Inverses
一个整数在整数集 Z 上没有乘法逆,但是可能会在余数类 $Z_6$ 上存在乘法逆。比如在 $Z_6$ 上,5 · 5 = 1,所以 5 的乘法逆是 5。
对于模 n 运算 $Z_n$,一个整数 r 是否有乘法逆,在于 n 和 r 是否互质。因为 gcd(n, r) = 1,根据扩展的欧几里得算法,存在 s, t ∈ Z,使得 1 = s · n + t · r 成立。如果该式子两边都模 n,那么 s · n 就会消失,即 1 = (t mod n) · r,所以 t mod n 就是 r 在 $Z_n$ 上的乘法逆。
费马小定理提供了一种计算 $Z_n$ 上的乘法逆的方法:对于素数 p 且 r < p,r^p ≡ r ( mod p ) ⇔ r^(p - 1) ≡ 1 ( mod p ) ⇔ r · r^( p- 2) ≡ 1 ( mod p ) ,所以 r 在模 p 运算 $Z_p$ 上的乘法逆就是 r^(p-2)
3 多项式
主要系数( leading coefficient):多项式中最高度的系数。
零多项式(zero polynomial):多项式的所有系数都是 0,即 p(x) = 0
一多项式(one polynomial):多项式中只有常数 1,其它所有系数都是 0,即 p(x) = 1
整数多项式(Integer Polynomials):多项式的系数必须都是整型,写作 Z[x]。
多项式长除法(Polynomial Long Division):整数多项式 A(x) = x^5 + 2x^3 − 9 ∈ Z[x] 可被整数多项式 B(x) = x^2 + 4x − 1 ∈ Z[x] 整除。因为 B 不是零多项式,且主要系数是 1,在整数上拥有乘法逆,因此可以应用多项式欧几里得算法。

质因子分解(prime factors):P = F1 · F2 · ... · Fk,其中,P 是多项式,F 是不可约多项式(类似于整数中的素数),被称为 P 的质因子(prime factor)
拉格朗日插值法(Lagrange Interpolation):度为 m 的多项式可由 m + 1 个点唯一确定。当多项式的系数拥有乘法逆时,可用拉格朗日插值法根据 m + 1 个点计算出度为 m 的多项式:

例如,对于点集 S = {(0, 4), (-2, 1), (2, 3)},可在实数域上计算出度为 2 的多项式:
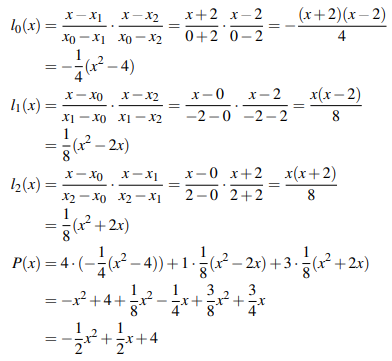
参考
The MoonMath Manual 第 3 章


没有评论