这篇文章上次修改于 617 天前,可能其部分内容已经发生变化,如有疑问可询问作者。
1 交换群 Commutative Groups
大白话
一个集合 G 和该集合上的某种二元运算。群 G 中的两个元素通过某种二元运算可得到该群中的另一个元素。群要满足一些性质,比如交换律、结合律、元素存在逆等。
定义
交换群 (G, ·) 包含两部分:
- 集合 G
- 二元运算 ·,即 G×G -> G,G 中的两个元素通过该二元运算后生成的元素仍然应该属于该 G
性质:交换律,结合律,存在中立元(任何 G 中的元素 g 与该元素结合后仍然是 g),每个元素都存在逆。
例如,(Z, +) 是一个群,Z 表示整数集合,映射关系 · 是加法 +,加法运算显然满足交换律和结合律,中立元素是 0(对于群 G 中的任何元素 g,g + 0 = g),g 的逆是 -g(对比如下定义,e = 0,g + (-g) = 0)。
原文

其它例子
$$ (Z_6, +) $$
如上式子也是群,$Z_6$ 表示模 6 的余数集合,满足:交换律和结合律,中立元素是 0,g 的逆是 6 - g,因为 g + (6 - g) = 6(对比如上定义,e = 6)。
有限群(finite group):群中的元素个数是有限的。群的个数称为阶(order)。如上例子 ($Z_6$, +) 的阶是 6。
循环群(cyclic group):存在生成器(generator),群 G 中的每个元素都可以通过对其多次应用群法则后可以得到。
- 例如,对于 (Z, +),生成器是 1,因为每个整数都可以通过重复加 1 得到。
- 例如,对于 ($Z_5^*$, ·),其中 $Z_5^*$ = $Z_5$ - {0},有 2^1 = 2,2^2 = 4,2^3 = 3,2^4 = 4,所以 2 是 ($Z_5^*$, ·) 的生成器; 3^1 = 3,3^2 = 4,3^3 = 2,3^4 = 1,所以 3 也是 ($Z_5^*$, ·) 的生成器。
- 对于模为 n ∈ N 且 n ≥ 2 的余数类群 ($Z_n$, +),生成器是 1,且群的个数有限,所以 ($Z_n$, +) 是阶为 n 的有限循环群。
1.1 指数映射 Exponential Map
如果 G 是一个阶为 n,生成器为 g ∈ G 的循环群,那么存在指数映射,将余数类群上的加法运算 ($Z_n$, +) 映射到 G 的群法则上:
$$ g^{(·)}: Z_n \rightarrow G, x\rightarrow g^x $$
标量乘法(Scalar multiplication):如果 (G, +) 被写作了加法形式,那么指数映射被称为标量乘法,形式如下:
$$ (·) · g: Z_n \rightarrow G ; x \rightarrow x · g $$
密码学算法通常使用阶 n 非常大的有限循环群,意味着对于非常大的余数类,通过生成器与自身的重复相乘来计算指数映射是不可行的 。如下算法 square and multiply 可在大约 k 步内计算指数映射,k 是指数的长度。

例如,3 ∈ $Z_5^∗$ 是 ($Z_5^∗$, ·) 的一个生成器,所以可将 $Z_4$ 上的加法运算映射到 $Z_5^∗$ 上的乘法运算:
$$ 3^{(·)}: Z_n \rightarrow Z_5^*, x\rightarrow 3^x $$
例如
$$ 3^{1+3+2} = 3^2 = 4 $$
先在 ($Z_4$, +) 上计算了 1 + 3 + 2,然后通过指数映射 $3^{(·)}$ 映射到 4
由于指数映射遵循群法则,也可以先在 $Z_5^*$ 上计算,结果是一样的:
$$ 3^1 · 3^3 · 3^2 = 3 · 2 · 4 = 1 · 4 = 4 $$
由于指数映射是遵循群法则的一对一映射,该映射对于 g 也有一个逆,叫做基为 g 的离散对数映射:
$$ log_g(·): G \rightarrow Z_n; x \rightarrow log_g(x) $$
离散对数映射在密码学中比较重要,因为存在有限循环群,计算指数映射比较快,而计算对数映射比较慢。
例如,对于前面例子中的指数映射 $3^{(·)}$,它的逆是基为 3 的对数映射:
$$ log_3{(·)}: Z_5^* \rightarrow Z_4;x \rightarrow log_3(x) $$
不同于指数映射 $3^{(·)}$,我们无法计算该映射,只能一个一个去试。例如,为了计算 $log_3(4)$,我们只能找一个 x ∈ $Z_4$,使得 $3^x$ = 4,这需要写下 $3^{(·)}$ 所有的 image:
$$ 3^0 = 1, 3^1 = 3, 3^2 = 4, 3^3 = 2 $$
由于 $log_3(·)$ 是 $3^{(·)}$ 的逆,可以通过这些 images 来计算离散对数:
$$ log3(1) = 0, log_3(2) = 3, log_3(3) = 1, log_3(4) = 2 $$
可以看到,计算对数映射是不可能的,我们只能写下指数映射到所有 image,但在现实世界中群上比较大的,不可能写出指数映射的所有 image
1.2 因子群 Factor Groups
有限循环群的基本定理(fundamental theorem of finite cyclic groups):如果 G 是阶为 n 的有限循环群,那么每个子群 $G^′$ 都是一个有限循环群,$G^′$ 的阶是 n 的一个因数。对于 n 的每个因子 k,G 都只有一个阶为 k 为子群。
对于阶为 n 都有限循环群 G,k 是 n 的一个因子,则 G[k] 为 G 的子群中唯一阶为 k 的有限循环群,称为 G 的因子群(factor group)。
密码协议通常假定存在素数阶的有限循环群。但在实际中,这些协议不是定义在素数阶的群上,这需要通过余因子清除(cofactor clearing)来确保运算不是在群本身,而是在它的(大)素数阶子群上。
可将 g ∈ G[k] 映射到 e ∈ G,通过与将 g 与自身乘 k 次:
$$ g^k = e $$
因此,如果 c := n div k 是 k 在 n 中的余因子(cofactor),则 g ∈ G 可映射到因子群 G[k] 上,通过将 g 与自身相乘 c 次。可定义如下映射,在密码学中被称为余因子清除(cofactor clearing):
$$ (·)^c: G \rightarrow G[k]: g \rightarrow g^c $$
例如,对于有限循环群 ($Z_5^*$, ·),阶是 4,4 有因子 1, 2, 4,且遵循有限循环群的基本定理,即有 3 个子群。$Z_5^*[1]$ = {1},$Z_5^*[4]$ = $Z_5^*$,$Z_5^*[2]$ = {1, 4}。$Z_5^*$ 不是素数阶群,4 唯一的素数因子是 2,2 在 4 中的余因子也是 2,所以得到余因子清除映射 $(·)^2: Z_5^* \rightarrow Z_5^*[2]$。将该映射应用到 $Z_5^*$,得到映射到 $Z_5^*[2]$ 中的元素:
$$ 1^2 = 1, 2^2 = 4, 3^2 = 4, 4^2 = 1 $$
1.3 配对 Parings
配对映射(Paring map):$G_1$,G_2$,G_3$ 均为交换群,配对映射定义如下:
$$ e(·, ·): G_1 \times G_2 \rightarrow G_3 $$
$(g_1, g_2)$ 取自 $G_1$ 和 $G_2$,将他们映射到 $G_3$,这种映射具有双线性(bilinearity),意味着对于 $g_1, g_1^{'} ∈ G_1$ 和 $g_1, g_2^{'} ∈ G_1$,有:
$$ e(g_1 · g_1^{'}, g_2) = e(g_1, g_2) · e(g_1^{'}, g_2) $$
和
$$ e(g_1, g_2 · g_2^{'}) = e(g_1, g_2) · e(g_1, g_2^{'}) $$
也就是说,双线性意味着先在 $G_3$ 上执行群运算然后再执行双线性映射,或者先执行双线性映射再在 $G_3$ 执行群运算都可以。
配对映射是非退化的(non-degenerate):如果配对的结果是 $G_3$ 中的中立元,则其中一个输入必然是 $G_1$ 或 $G_2$ 中的中立元。
例如,$G_1$,$G_2$,$G_3$ 都是 (Z, +),如下映射是非退化的配对:
$$ e(·, ·): Z \times Z \rightarrow Z (a, b) \rightarrow a · b $$
非线性遵循加法分配律,即 $e(a + b, c) = (a + b)· c = a · c + b · c = e(a, c) + e(b, c)$
假设 $e(a, b) = 0$,那么 $a · b = 0$,意味着 $a$ 或 $b$ 必然是 0 。
1.4 群上的困难问题
离散对数困难问题 DL
离散对数问题(Discrete Logarithm Problem,DLP):对于阶为 r,生成器为 g 的有限循环群 G,存在指数映射 $g^{(·)}: Z_r \rightarrow G; x \rightarrow g^x$ 将余数类 $Z_r$ 群映射到 G 上。Discrete Logarithm Problem 的任务是找到该映射的逆,也就是找到 $x ∈ Z_r $,使得对于给定 $h, g ∈ G$ 满足:
$$ h = g^x $$
假设在有的群上求解 DLP 不可行,这样的群称为 DL-secure 群。
公钥加密((Public key cryptography): 对于私钥 $sk ∈ Z_r $,相应的公钥为 $pk ∈ g^{sk}$。由于离散对数问题被认为是难道,所以不可能从公钥解出私钥,即找到如下问题的解是比较难的:
$$ pk = g^x $$
判决性 Diffie–Hellman 问题 DDH
The Decisional Diffie–Hellman (DDH):对于阶为 n,生成器为 g 的有限循环群 G,DDH 是给定三元组 $(g^a, g^b, g^c)$ 后,无法区分 $(g^a, g^b, g^{ab})$,其中 $ a, b, c ∈ Z_r$。这种情况下,称 G 为 DDH-secure 群。
DDH-security 是比 DL-security 强的假设,如果 DDH 不可解,那么 DLP 也不可解,反之不一定成立。
计算性 Diffie–Hellman 问题 CDH
The Computational Diffie–Hellman Assumption:G 是阶为 n,生成器为 g 的有限循环群,对于 $a, b ∈ Z_r $,如果 $g, g^a, g^b$ 已知,但是 $a$,$b$ 未知,则无法计算 $g^{ab}$。这种情况下,称 G 为 CDH-secure 群。
CDH 假设弱于 DDH 假设,有的群满足 CDH 但是不满足 DDH,而不存在有的群满足 DDH 但不满足 CDH。
1.5 哈希到群 Hashing to Groups
哈希函数
哈希函数是将任意长度的二进制串 $\left\{0, 1 \right\}^*$ 映射到长度为 k 的二进制串 $\left\{0, 1 \right\}^k$:
$$ H: \left\{0, 1\right\}^* \rightarrow \left\{0, 1\right\}^k $$
哈希函数 H 返回的值为像(images),也称哈希值。
密码学函数的性质
- 抗原像(preimage-resistance):给定 $\left\{0, 1 \right\}^k$,无法找到字符串 $x ∈ \left\{0, 1 \right\}^*$ 使得 $H(x) = y$。
- 抗碰撞(collision resistance)
- diffusion:输入中的微小变化会导致输出中的巨大差异
SHA256 是一个密码学安全的哈希函数:$SHA256: \left\{0, 1 \right\}^* \rightarrow \left\{0, 1\right\}^{256}$
空字符串的 SHA256 值为:
$$ SHA256(<>) = e3b0c44298 f c1c149a f b f 4c8996 f b92427ae41e4649b934ca495991b7852b855 $$
哈希到循环群
哈希到群(hash-to-group)函数是一个确定性映射:$SHA256: \left\{0, 1\right\}^* \rightarrow G$
Pedersen Hashes
Pedersen 哈希函数(Pedersen Hash Function):$j$ 是一个整数,$G$ 是有阶为 $n$ 的限循环群,$\left\{g_1, ..., g_j \right\} ⊂ G$ 是一个均匀随机分部的$G$ 的生成器的集合
$$ H_\left\{g_1, ..., g_j \right\}:(Z_r)^j \rightarrow G: (x_1, ..., x_j) \rightarrow \prod_{i=1}^jg_i^{x_i} $$
如果 G 是 DL-secure 的,那么 Pedersen 哈希函数是抗碰撞的。
$\left\{g_1, ..., g_j \right\}$ 必须均匀随机分别,任何两个生成器之间不能存在离散对数关系,即必须要避免 $g_h = (g_i)^x$,其中 $x ∈ Z_n$ 。
例如,对于 Pedersen’s 哈希函数 $H_\left\{2, 3\right\}: Z_4 \times Z_4 \rightarrow Z_5^*; (x, y) \rightarrow 2^x · 3^y$,可以算出 $H_\left\{2, 3\right\}(1, 3) = 2^1 · 3^3 = 2 · 2 = 4$
哈希函数如 $SHA256(s)$ 可以和 $H_\left\{2, 3\right\}$ 一起定义一个 hash-to-group 函数。将 $SHA256(s)$ 最低的两位插入到 $H_\left\{2, 3\right\}$ 以得到 $F_5^*$ 中的元素。如下定义了 hash-to-group 函数
$$ $SHA256\_H_\left\{2, 3\right\}: \left\{0, 1\right\} \rightarrow Z_5^*; 2^{SHA256(s)_0} · 3^{SHA256(s)_1} $$
我们知道,$SHA256(<>)_0 = 1$,$SHA256(<>)_1 = 0$,所以 $SHA256\_H_{2, 3}(<>) = 2^1 · 3^0$
Pseudorandom Function Families in DDH-secure groups
G 是一个 DDH-secure 循环群,阶为 n,生成器为 g,$\left\{a_0, a_1, ..., a_k\right\} ⊂ Z_n^*$ 是从在模 n 算术可逆的数字中生成的一个均匀随机集合。以种子 $\left\{a_0, a_1, ..., a_k\right\}$ 作为参数的 Pseudorandom 函数族为:
$$ F_{\left\{a_0, a_1, ..., a_k\right\}}: \left\{0, 1\right\}^{k+1} \rightarrow G: (b_0, ..., b_k) \rightarrow g^{b_0}\prod_{i=1}^ka_i^{b_i} $$
2 交换环 Commutative Rings
大白话
在交换群的基础上,多了一种二元运算。
定义
拥有单元的交换环(commutative rings with unit)(R, +, ·, 1) 包含 4 部分
- 集合 R
- 两种二元运算 + 和 ·
- 新运算单元(unit) 1:新运算存在中立元,即对于所有元素 g,有 1 · g = g
性质:
- (R, +) 是交换群,中立元是 0
- 新运算满足交换律
- 新运算存在中立元 1,即对于所有元素 g,有 1 · g = g
- 新运算满足结合律
- 新运算满足分配律
例如,(Z, +, ·, 1) 是一个交换环,其中 Z 表示整数集合,+ 表示加法运算,· 表示乘法运算,1 表示数字 1。
需注意,(Z, ·) 无法构成群,因为整数不存在乘法逆。
原文

多项式环(Ring of Polynomials):多项式的系数 R 必须一个拥有单元的交换环,因为我们需加法、乘法、可交换和 R 存在一个单元来获得我们所期望的性质。在此基础上,如果 1 是乘法单元,则成该环为系数为R的多项式环(ring of polynomials with coefficients in R)
群生成器指数中的多项式评估(Polynomial evaluation in the exponent of group generators):在许多零知识协议中,一个关键的是能够将计算编码为多项式,然后通过评估某些密码群的“指数”中的多项式来隐藏该计算的信息。
为了理解上述原理,再来看下指数映射。如果 G 是有限循环群,阶为 n,生成器为 g ∈ G,($Z_n$, +, ·) 是以如下方式对应 G 的环:
$$ g^{x+y} = g^x · g^y, g^{x·y} = (g^x)^y, x, y ∈ Z_n $$
设 $p ∈ z_n[x]$ 是一个多项式 $p(x) = a_m · x^m + a_{m-1}x^{m-1} + ... + a_1x + a_0$,$s ∈ z_n$ 是一个评估点,那么有:
$$ \begin{align} g^{p(s)} &= g^{a_m · x^m + a_{m-1}x^{m-1} + ... + a_1x + a_0} \\ &= (g^{s^m})^{a_m} · (g^{s^{m-1}})^{a_m} ·...·(g^s)^{a_1} · g^{a_0} \\ \end{align} $$
可以在 g 的指数中“秘密”评估点 s 处计算任何度小于 m 的多项式 p,而不需要知道任何关于 s 的知识。假设 G 是 DL-group,只要给定 $\left\{g, g^s, ...,g^{s^m} \right\}$,但是不需要给定 s,就可以算出 $g^{p(s)}$,但不会算出 s。
例如,对于如下指数映射
$$ 3^{(·)}: Z_4 \rightarrow Z_5^*, x\rightarrow 3^x $$
从 $z_4[x]$ 中选出多项式 $p(x) = 2x^2 + 3x + 1$,先在 s = 2 处评估多项式,然后将结果写到指数:
$$ \begin{align} 3^{p(2)} &= 3^{2·2^2 + 3·2 + 1} \\ &= 3^{2·0 + 2 + 1} \\ &= 3^3 \\ &= 2 \end{align} $$
结果是 2,但是不会获得关于 s 的任何知识。
2.1 哈希到模代数 Hashing into Modular Arithmetic
n 是模数,k = |n| 是 n 的宽度,那么每个长度为 k - 1 的二进制数字 $z = <b_0, b_1, ..., b_{k-2}>$ 的范围为 $0 \le z \le 2^{k-1} - 1 < n$,所以 z 属于 $Z_n$,$H: \left\{0, 1 \right\}^* \rightarrow \left\{0, 1 \right\}^{k-1}$ 是哈希到环的哈希函数:
$$ H_{|n|_2-1}: \left\{0, 1 \right\}^* \rightarrow Z_r : s \rightarrow H(s)_0 · 2^0 + H(s)_1 · 2^1 + . . . + H(s)_{k−2} · 2^{k−2} $$
$|n|_2$ 表示 n 的二进制宽度。该哈希函数的缺点是哈希值在 $Z_n$ 上的分布不一定是均匀的。如果 $n > 2^{k-1}$,则 $H_{|n|_2 - 1}$ 不会哈希到 $z \ge 2^{k-1}$。所以 n 应该要非常接近于 $2^{k-1}$ 才能确保分布均匀。该哈希函数的优点是抗原像和抗碰撞。
另一个被广泛使用的哈希到 $Z_n$ 的方法是:$|n|_2 = k_1$,$k_2 \ge k_1$,有 $H: \left\{0, 1 \right\}^* \rightarrow \left\{0, 1 \right\}^{k_2} $ ,构造如下:
$$ H_{mod_n}' : \left\{0, 1 \right\}^* \rightarrow Z_n : s \rightarrow (H(s)_0 · 2^0 + H(s)_1 · 2^1 + ... + H(s)_{k_2} · 2^{k_2}) \space mod \space n $$
该哈希函数的缺点是计算量大,在 $Z_n$ 上的分布可能不均匀,取决于 $2^{k_2 + 1}$ mod n。优点是抗原像和抗碰撞。
The “try-and-increment” method
第 3 种是 “try-and-increment” 方法。定义 z ∈ Z,对于任何 H(s) 有:
$$ z = H(s)_0 · 2^0 + H(s)_1 · 2^1 + ... + H(s)_{k_2} · 2^{k} $$
为了映射到 $Z_n$,先计算 z,然后看是否 $z ∈ Z_n$,如果是,则哈希结束;否则,修改字符串 s,然后再次计算 z,直到 $z ∈ Z_n$。一种修改 s 的方式是,将 s 和一个 bit 计数器拼接。算法如下:

如果 k 足够大,且 n 接近于 $2^{k+1}$,则 z < n 的概率较大,则循环基本只需要执行 1 次
3 域 Fields
大白话
在交换环的基础上,元素拥有乘法逆,即第二种运算和集合可以构成群。
定义
域 (F, + , ·) 包含三部分:
- 集合 F
- 两种二元运算 + 和 ·
性质:
- (F, +) 是交换群,中立元是 0
- (F - {0}, ·) 是交换群,中立元是 1
- 满足分配律:g1 · (g2 + g3) = g1 · g2 + g1 · g3
原文

域 F 的特征(characteristic)表示为 char(F),是最小自然数 n ≥ 1,乘法中立元 1 的 n 次叠加结果等于零,即 $\sum_{i=1}^n1 = 0$。如果 n > 0 存在,则称域拥有一个有限特征(finite characteristic)。如果每个 1 的有限和都不等于 0,则称域有特征 0。
例如,(Q, + , ·) 是一个域,Q 表示实数集合,+ 表示加法运算,· 表示乘法运算。除 0 外,每个实数都拥有乘法逆。因为不存在自然数 n ∈ N 使得 $\sum_{j=0}^n1 = 0$ 位于实数集合中,所以域 Q 的特征是 char(Q) = 0
素数域 Preime Fields
如果模是一个素数,余数类 $Z_n$ 不仅是环,还是域。由于 $\sum_{j=0}^n1 = 0$ 位于 $Z_n$ 中,所以域拥有有限特征 n。
素数域:$(Z_p, +, ·)$ 是一个模 p 运算上的域,p ∈ P 是一个素数,我们称该域为素数域,特征为 p。为了区分,$(Z_p, +, ·)$ 表示为 $(F_p, +, ·)$。
素数域上,x 的加法逆是 -x = p - x mod p,x != 0 时,乘法逆为 $x^{-1} = x^{p-2}$。
最小的域是 $F_2$,特征为 2,它是个素数域。
3.1 平方根 Square Roots
在素数域中,一个拥有平方根 x 的元素 y 称为二次剩余(quadratic residue),x 为平方根(square root),一个没有平方根的元素称为二次无剩余(quadratic non-residue)。只有平方数可以位于椭圆曲线上。
对于 $x ∈ F_p$,如果 y != 0,则有两个根 $\sqrt y = \left\{x, p-x\right\}$。前一个为正平方根(positive square root),后一个为负平方根(negative square root)。$F_p$ 中有 (p + 1) / 2 个 quadratic residue,(p - 1) / 2 个 quadratic non-residue。
Legendre symbol
$y ∈ F_p$
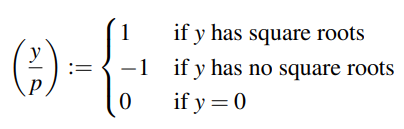
例如对于 $F_5$,有
$$ \frac{0}{5} = 0, \frac{1}{5} = 1, \frac{2}{5} = -1, \frac{3}{5} = -1, \frac{4}{5} = 1 $$
欧拉标准(Euler criterion)提供了一种计算 Legendre symbol 的方法。对于奇素数 $p ∈ P_{>=3}$ 和 $y ∈ F_p$,Legendre symbol 用如下方式计算:
$$ (\frac{y}{p}) = y^{\frac{p-1}{2}} $$
3.2 素数域扩展 Prime Field Extension
给定素数 p ∈ P,自然数 m ∈ N,度为 m 的不可约多项式 $P ∈F_p[x]$,其系数选自素数域 $F_p$,一个素数域扩展 $(F_{p^m}, +, ·)$ 定义如下。
$F_{p^m}$ 是度小于 m 的所有多项式集合:
$$ F_{p^m} = \left\{a_{m-1}x^{m-1} + a_{m-2}x^{m-2} + ... + a_1x + a_0 | a_i ∈ F_p\right\} $$
$F_{p^m}$ 的特征是 p,有 $\sum_{j=0}^p1 = 0$。$F_{p^m}$ 的阶是 $p^m$,因为 $F_{p^m}$ 的每个元素都是度小于 m 的多项式,每个系数都有 p 种选择。当将 $F_{p^m}$ 中的每个元素的度都限制为 0 时, $F_{p^m}$ 就是 $F_p$,所以 $F_p$ 是 $F_{p^m}$ 的子域(subfield)。
$F_{p^m}$ 的构建依赖于不可约多项式 $P$ 的选择,但对于 $P$ 的不同选择,$F_{p^m}$ 是同构的,即不同的 $F_{p^m}$ 之间拥有一一映射关系。从实现的角度,应该挑选易于计算的 $P$。
类似于素数域 $F_P$ 是整数环中的整数除以一个素数 p 后的余数集合,素数域扩展 $F_{p^m}$ 是 $F_p[x]$ 环中的多项式 $F_p[x]$ 除以一个度为 m 都不可约多项式后的余数多项式集合。
如果 $m_1$ 整除 $m_2$,那么 $F_{p^{m_2}}$ 是 $F_{p^{m_1}}$ 的扩展域。
例如,$F_{2^3}$ 中的元素有:
[0,0,0]: 0 [0,0,1]: x2
[1,0,0]: 1 [1,0,1]: x2 + 1
[0,1,0]: x [0,1,1]: x2 + x
[1,1,0]: x + 1 [1,1,1]: x2 + x + 13.3 射影平面 Projective Planes
射影平面通过包含无穷点而扩展了普通 Euclidean 平面的概念。例如,在射影平中,平行线交于无穷点处。
F 是域,射影平面 $FP^2$ 由形如 [X : Y : Z] 的点构成, 其中 (X, Y, Z) ∈ $F^3$ 是不全为 0 的元素:
$$ FP^2 := \left\{[X : Y : Z] \space | \space (X,Y, Z) ∈ F^3 \space with \space (X,Y, Z) \ne (0, 0, 0) \right\} $$
并且,对任何非零的 k ∈ $F^*$,规定 $[kX : kY: kZ]=[X : Y : Z]$(对于有限域 $F_p$,$kX$ 是指 $kX$ mod p )
有限域 $F_{p^m}$ 上的投影面中的元素个数为 $p^{2m} + p^m + 1$。
将所有形如 [X : Y : 1] 的点称为仿射点,而将形如 [X : Y : 0] 的点称为无穷远点;这些无穷远点构成一条射影直线 [1 : 0 : 0],也就是无穷远线。
参考
The MoonMath Manual 第 4 章
https://coders-errand.com/zk-snarks-and-their-algebraic-structure-part-4/


没有评论