这篇文章上次修改于 561 天前，可能其部分内容已经发生变化，如有疑问可询问作者。

1 什么是 SCEV

Scalar Evolution（SCEV）用于分析循环中的标量（scalar）是如何变化的（evolution）。

SCEV 是 LLVM 中一个很重要的 analysis pass，可识别 general induction variables。该 analysis 主要用于 induction variable substitution 和 strength reduction。

例子：

void foo(int *a, int n, int k) {
    int t = 0;
    for (int i = 0; i < n; i++) {
        t = t + k;
    }
    *a = t;
}

$t$ 的初值是 0，每次循环都会对 $t$ 加 $k$，这便是 $t$ 的演化。

但只有 $t$ 的终值会被 *a = t 用到，那么是否有一种方法可以直接算出 $t$ 的终值，而不必进入循环中一步一步去算？

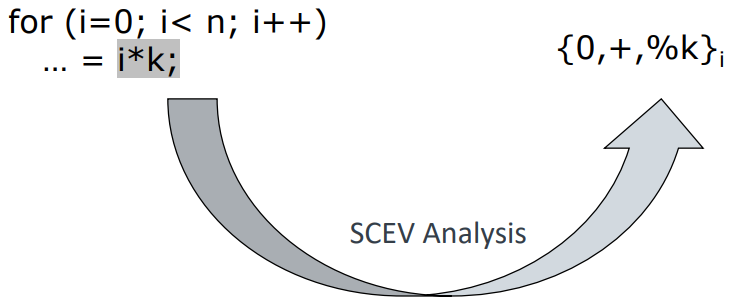
下图使用了 SCEV 分析结果后进行优化的例子：

优化后的 IR 直接用 t = n * k 得到了 $t$ 的终值，从而去掉了 for 循环。

另外一个例子：

优化后的 IR 用加法代替了乘法运算。

以上优化是如何是如何做到的？下一章看下 SCEV 是如何对循环中的变量进行建模的。

2 SCEV 的数学框架 -- Chains of Recurrences

SCEV 采用非循环表达式对循环中的变量建模，该表达式称为 Chains of Recurrences (CR)。

2.1 Basic Recurrences

int f = k0;
for (int i = 0; i < n; i++) {
    … = f ;
    f = f + k1;
}

其中，$k_0$ 和 $k_1$ 是循环不变量，$f$ 的递推公式为：

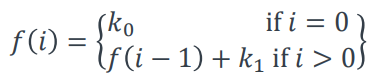
basic recurrence = {$k_0$, +, $k_1$}，表示初值是 $k_0$，每次递增 $k_1$。

BR 形式化表示：$\left\{a_0, \bigodot, a_1\right\}$

$a_0$ 是初值，是一个常数
$\bigodot$ 是一个二元运算，$\bigodot$ ∈ {+, ∗}
$a_1$ 是步长，是一个常数。

例如，BR = {3, +, 7} 可以生成序列 3, 10, 17, ...

## 2.2 Chain Recurrences

与 basic recurrence 相比，chain recurrrence 中的步长可能不是常量，而是另一个 basic recurrence。

例如 {1, +, {3, +, 7}} 指一个序列的初始值是 1，以另一个 BR = {3, +, 7} 作为步长进行增加：

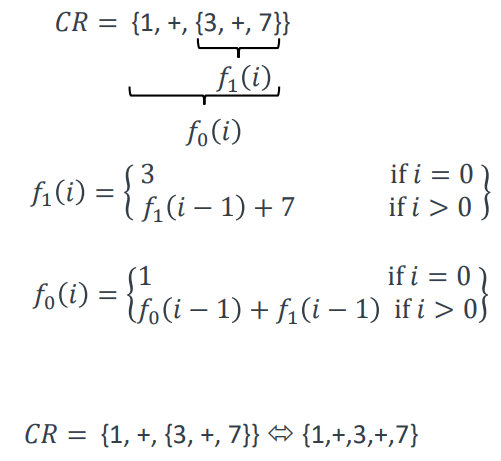
上述式子比较抽象，写成代码形式会更容易理解变量 i 是如何变化的：

// SCEV for i: {1, +, 3, +, 7} 
int i = 1;
int j = 3;
while (i < n) {
    i += j;
    j += 7;
}

CR 形式化表示：$\left\{a_0, \bigodot_1, a_1, \bigodot_2, a_2 ..., \bigodot_n, a_n \right\}$

2.3 构建 CR

常用的运算规则：

$ C + \left\{e, + f \right\} \rightarrow \left\{C + e, +, f\right\}$，$C$ 是循环不变的
例如 12 + {7, 3} => {19, +, 3}
$C * \left\{e, +, f\right\} \rightarrow \left\{C * e, +, C * f\right\}$，$C$ 是循环不变的
例如 12 * {7, +, 3} => {84, +, 36}
$\left\{e, +, f\right\} + \left\{g, +, h\right\} \rightarrow \left\{e + g, +, f + h\right\}$
例如 {7, +, 3} + {1, +, 1} => {8, +, 4}
$\left\{e, +, f \right\} * \left\{g, +, h\right\} \rightarrow \left\{e * g, +, h * \left\{ e, +, f\right\} + f * \left\{ g, +, h\right\} + f * h \right\}$
如果 f 和 h 为常数，则公式还可表示为 $\left\{e * g, +, e * h + f * g + f * h, +, 2 * f * h\right\}$
例如 {0, +, 1} * {0, +, 1} => {0, +, 1, +, 2}

有了上述规则，就可以通过已有变量的 CR 推出其它变量的 CR，例如：

前面的规则比较好理解，如果有兴趣的话，可以看下最后一个规则的推导：

设 $x = \left\{e, +, f\right\}$，$y = \left\{g, +, h\right\}$，则 $start_{xy} = eg$，

$$ \begin{align} step_{xy} & = x_ky_k - x_{k-1}y_{k-1} \\ & = (x_{k-1} + f)(y_{k-1} + h) - x_{k-1}y_{k-1} \\ & = x_{k-1}y_{k-1} + x_{k-1}h + fy_{k-1} + fh - x_{k-1}y_{k-1} \\ & = x_{k-1}h + fy_{k-1} + fh \end{align} $$

所以

$$ \begin{align} xy & = \left\{eg, +, hx + fy + fh\right\} \\ & = \left\{eg, +, h\left\{ e, +, f\right\} + f\left\{ g, +, h\right\} + fh \right\} \\ \end{align} $$

参考文献 [7] 给出了另一种推导方式。

3 SCEV 应用示例

计算 $sum$：

int sum = 0;
for (int i = 1; i <= n; i++) {
    sum += i * i * i;
}

其中，$i * i * i$ 的 CR 可用如下式子简化

$$ \begin{align} i * i * i &= \left\{1, +, 1\right\} * \left\{1, +, 1\right\} * \left\{1, +, 1\right\}\\ &= \left\{1, +, \left\{3, +, 2\right\}\right\} * \left\{1, +, 1\right\}\\ &= \left\{1, +, \left\{1, +, 3, +, 2 \right\} + \left\{3, +, 2 \right\} * \left\{1, +, 1 \right\} + \left\{3, +, 2\right\} \right\}\\ &= \left\{1, +, \left\{1, +, 3, +, 2 \right\} + \left\{3, +, 7, +, 4 \right\} + \left\{3, +, 2\right\} \right\}\\ &= \left\{1, +, \left\{4, +, \left\{10, +, 6 \right\}\right\} + \left\{3, +, 2\right\} \right\}\\ &= \left\{1, +, \left\{7, +, \left\{12, +, 6 \right\}\right\} \right\}\\ &= \left\{1, +, 7, +, 12, +, 6 \right\}\\ \end{align} $$

所以

$$ sum = \left\{0, +, i * i * i\right\} = \left\{0, +, 1, +, 7, +, 12, +, 6\right\} $$

下图中的方式也可以计算出 CR

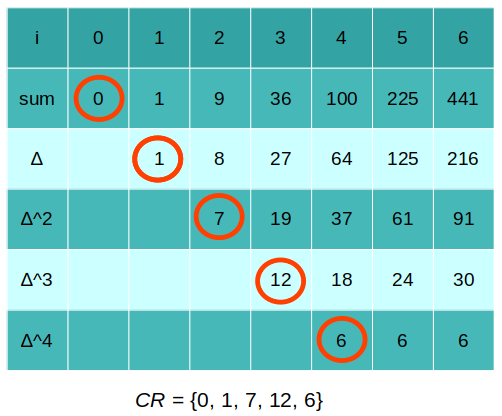
第 1 行表示循环次数，第 2 行是 sum 的值，第 3 行是两次循环之间的 sum 的差值 $\delta$，第 4 行是两次循环之间 $\delta$ 的差值 $\delta^2$，第 5 行是两次循环之间 $\delta^2$ 的差值 $\delta^3$，第 5 行是两次循环之间 $\delta^3$ 的差值 $\delta^4$。

体现在代码上：

int sum = 0;
int t1 = 1;
int t2 = 7;
int t3 = 12;
for (int i = 1; i <= count; i++) {
    // sum += i * i * i;
    sum += t1;
    t1 += t2;
    t2 += t3;
    t3 += 6;
}

用加法运算取代了昂贵的乘法运算。

但是发现，求和过程中，虽然 $sum$ 在不断变化，但是不需要追踪它的变化，只需要知道它的终值即可。

其实，有了 CR 后，我们可以直接用数学的方法推出该循环执行了 $i$ 次后 $sum$ 是多少。例如，$var$ = {0, +, 3}，可以直接算出循环 3 次后，$var$ = 9。对于一般情况 $var = \left\{a_0, +, a_1, +, ..., +, a_n\right\}$，则第 $i$ 次循环后 $var$ 的值为

$$ \begin{align} var(i) & = \sum_{j=0}^n a_j C_i^j \\ & = a_0 + a_1i + a_2\frac{i(i-1)}{2!} + ... + a_n\frac{i(i-1)...(i-n-1)}{n!} \end{align} $$

推导过程见参考文献 [7]。

可简单理解为：
$a_0$ 只有在最初时被加了 1 = $C_i^0$ 次
$a_1$ 在每个循环中都被加了 i = $C_i^1$ 次
$a_2$ 在第 2 个循环被加了 1 次，第 3 个循环被加了 2 次，...，共被加了 $i * (i - 1) / 2 = C_i^2$
$a_j$ 共被加了 $C_i^j$
所以 $var(i) = \sum_{j=0}^n a_j C_i^j$

那么，对于 $sum$= {0, +, 1, +, 7, +, 12, +, 6}，可以直接得到第 $i$ 次循环后

$$ \begin{align} sum(i) & = 0 + i + \frac{7i(i-1)}{2!} + \frac{12i(i-1)(i-2)}{3!} + \frac{6i(i-1)(i-2)(i-3)}{4!} \\ & = i + \frac{7i(i-1)}{2} + 2i(i-1)(i-2) + \frac{i(i-1)(i-2)(i-3)}{2} \\ \end{align} $$

编译器只需要生成类似生成计算上述式子的代码即可，从而将时间复杂度由 O(n) 降到 O(1)。

使用如下命令可查看优化前的代码：

$ clang -emit-llvm -S sum.c -o sum.ll

使用如下命令可查看优化后的代码：

$ clang -emit-llvm -O3 -S sum.c -o sum.ll

使用如下命令可查看 SCEV 分析：

$ opt -analyze -scalar-evolution sum.ll

使用如下命令可以得到更为简短的输出：

$ opt -analyze -scalar-evolution -scalar-evolution-classify-expressions=0 sum.ll

4 LLVM 中的 SCEV

4.1 SCEV 接口使用示例

int simpleLoop(int n) {
    int sum = 0;
    for (int i = 0; i <= n; i++) {
        sum += i;
    }
    return sum;
}

getSCEV(i) = <0, +, 1><nsw, nw>
getExitCount(latchBB) = n
getSCEVAtScope(sum, nullptr) = n * (n + 1) / 2，有助于减少一些小的循环
getLoopDisposition(n) = Invariant
isKnownNonNegative(i) = true

4.2 规范 loop

先将循环规范后，再供 SCEV 使用。

循环

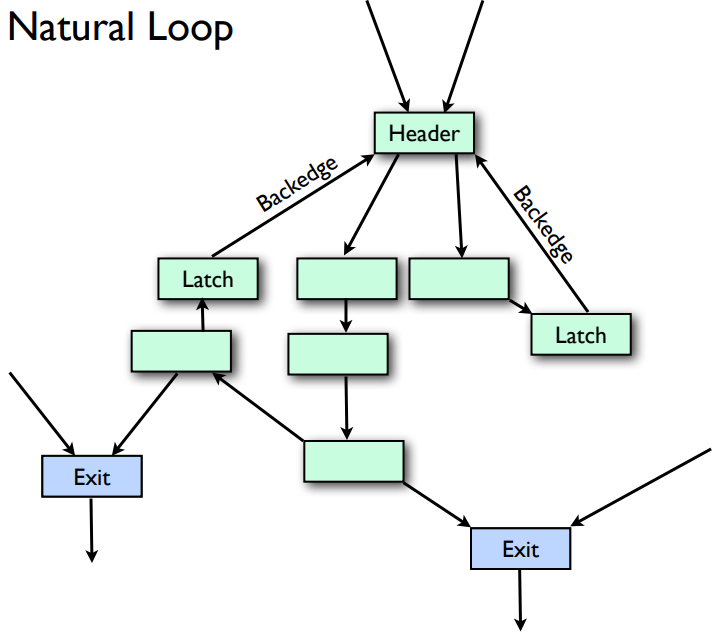
header：循环入口节点

backedge：回到 header 的边

latch：backage 的起始节点

exiting：后继位于循环外部的节点

exit：前继位于循环内部的节点

规范后的循环

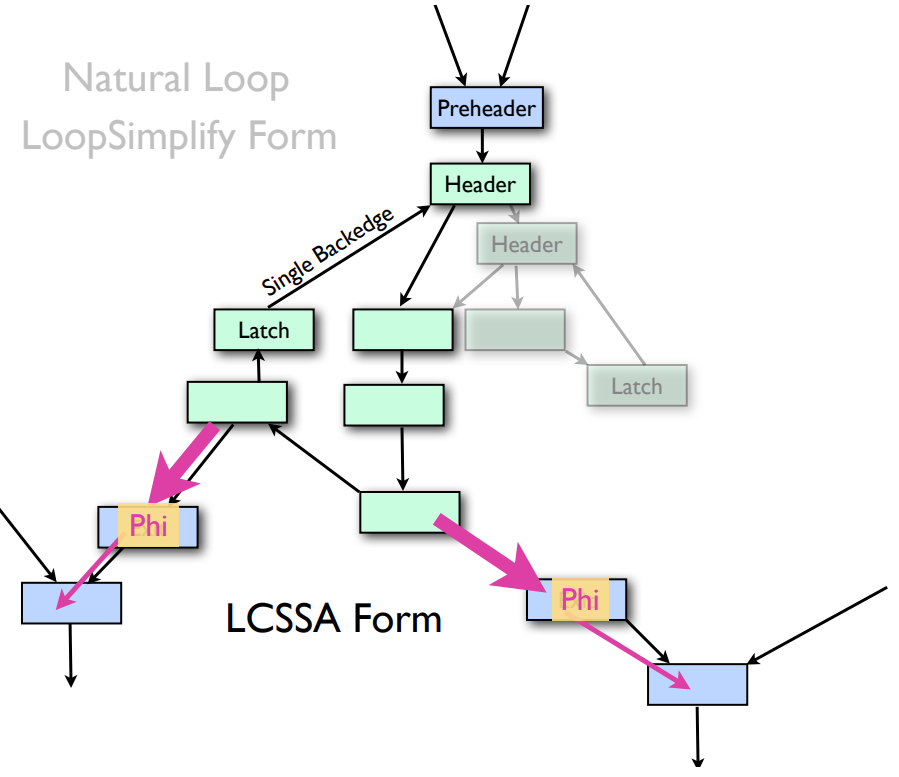
Preheader
header 节点的唯一前继，支配（dominate）整个 loop
Single Backedge
Dedicated Exit
Loop-closed SSA 在循环边界处为在循环内部定义但在循环外部使用的变量插入 phi 指令
- 可确保循环内部和外部优化的独立
- 更快地将 IR 转换成 SSA 形式

4.3 SCEV 函数

getSCEV(V)

生成变量 V 的 SCEV 表达式。

getSCEVAtScope(S, L)

返回循环 L 中变量 S 的 SCEV 表达式。如果 S 位于 L 外，则可结合 getExitCount 计算 S 的退出值。

SCEV 表达式支持：

整型和指针型，不适用于浮点型
整数类型转换：zext, sext, trunc
运算：min, max, add, mul, udiv，不适用于 sdiv

SCEV 表达式可嵌套，叶子节点是常数或者“unknown”。

不同于 IR 指令，SCEV 表达式支持多个操作数，比如 %a + %b + %c。

SCEV 表达式在构建的时候就会被规范化，比如会将 %a + (%b + %c) 替换为 %a + %b + %c，会将 %a + 1 替换为 1 + %a，会将 %a - %b 替换为 (-1 * %b) + %a。所以给定一系列操作数和类型，只会对应唯一的 SCEV 表达式。如果想比较两个 SCEV 表达式是否相同，只需要比较它们的指针是否相同即可。

getExitCount(L, ExitBB, ExitKind)

对于循环 L，返回某个退出块 ExitBB 的退出计数（backedge-taken count, BE count）。

BE count 统计了 loop backedge 在循环退出前执行了多少次。
trip count 是 loop header 被执行的次数，通常被称为迭代次数。
两者比较：tripe count = BE count + 1。如果循环在第一次迭代就退出，则 BE = 0，trip count = 1。使用 BE count 的原因是它的 bit-width 和控制循环的 IV（induction variable）宽度一样，而 tripe count 中的加 1 操作可能会导致溢出。

注意，如果循环异常退出，退出计数不会因此发生改变。如果循环从未从该出口退出过，该值可能是无限大，或者至少大于其它出口的退出计数。它只是一个近似实用的函数。

ExitKind 有三种模式：
exact，仅适用于只有一个出口的循环。
symbolic max：可以认为是所有出口中的最大退出计数。
constant max：是 symbolic max 的常量上限，常见的值是 -1（或者在无符号数情况下是 UINT_MAX）。

有了 BE count，就可以算出”exit value“或”SCEV at scope" 。例如，有 SCEV 为 {2, +, 3}，BE count 为 -1 + %n，那么退出值为 2 + 3 (-1 + %n) 或 -1 + (3 %n)

Predicate checking

isKnownPredicate / isKnowX：是其它断言的基础
isLoopEntryGuardedByCond / isLoopBackedgeGuardedByCond：检查在循环入口或循环 backedge 处，谓词是否是否成立。这两个函数结合在一起，有助于将表达式简化为循环不变的，是循环转换时非常有用的谓词。

LoopDisposition / Invariance / dominates

对于给定值，返回它是否”可能“是潜在循环不变的，是否是支配的，主要用于 SCEV 程序内部。

注意，这里的“潜在循环不变”比较微妙，SCEV 级别上的 domination / invariance 和 IR 级别上的会有一些不同。例如：

/*
for (int i = 0; i < end; i++) {
    d = a / b;
}
*/

loop:
  %iv = phi i32 [ 0, %preheader ], [ %iv.next, %loop.latch ]
  %iv.next = add i32 %iv, 1
  %cmp = icmp ne i32 %iv.next, %end
  br i1 %cmp, label %loop.latch, label %exit

loop.latch:
  %div = udiv i32 %a, %b    ; operands defined outside of loop
  br label %loop

udiv i32 %a, %b 不能被提到循环外，因为如果循环在第一次迭代就退出的话，udiv 是不会被执行到的。如果向 LoopInfo 询问 %div 对于 %loop 是否是循环不变的，答案是否。

但是，如果看 SCEV 表达式 %a /u %b，那么它对于 %loop 是循环不变的，可以提到循环外面。所以 SCEV 级别上的 domination / invariance 要强于 IR 级别。

SCEVExpander

有时候需要从 SCEV 表达式回到 IR 指令，比如在 IR 中计算退出计数或退出值，这可被 SCEVExpander 处理，它可生成一些必要的指令来计算 SCEV 表达式的值。

在扩展前，要检查两件事：