这篇文章上次修改于 487 天前，可能其部分内容已经发生变化，如有疑问可询问作者。

1.1 Merkle Tree

1 Merkle Tree

叶节点（leaf）存储数据或其哈希值，中间节点（non leaf）是它的两个孩子节点内容的哈希值。只要叶节点有任何变动，都会传递到其父节点，一直到 root。

2023-06-09T09:27:57.png

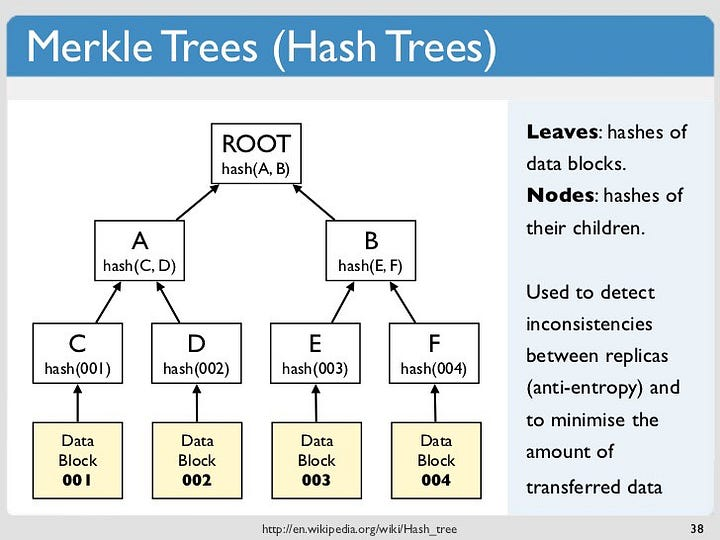
图片来源：https://en.wikipedia.org/wiki/Merkle_tree

1.2 Merkle Proof

2023-06-09T09:28:17.png

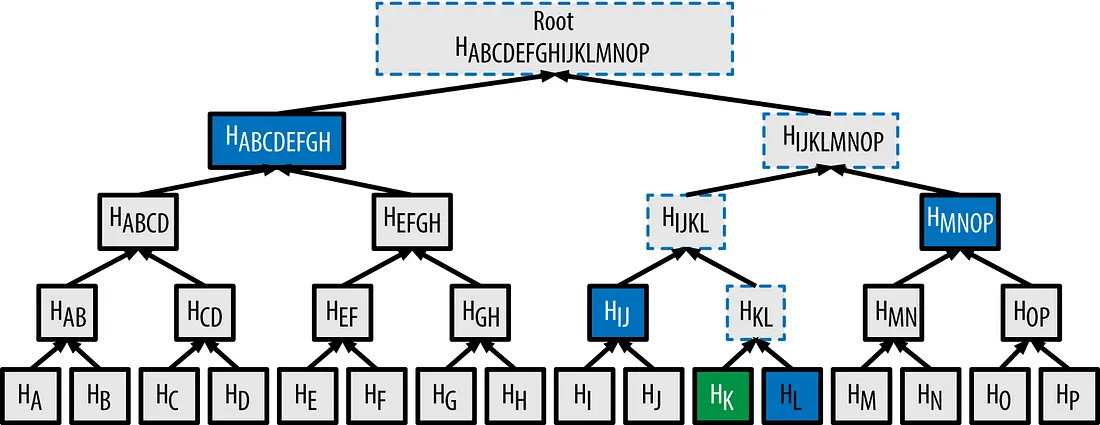
图片来源：https://medium.com/crypto-0-nite/merkle-proofs-explained-6dd429623dc5

K 的 proof 包含了上图中蓝色的部分，即 H(L), H(IJ), H(MNOP) 和 H(ABCDEFGH) ，通过 proof 和 K 可以计算出 root，与真正的 root 比对，如果一致，则说明 K 存在。

1.3 Merkle Tree 优点

快速检查数据一致性
对于 P2P 网络，数据可能存在于多个地方，验证数据完整性步骤：
1. 计算机 A 将文件的哈希发送到计算机 B
2. 计算机 B 比对该哈希和 Merkle Tree 中的 root 是否一致，如果一致则结束，否则转到步骤 3
3. 计算机 B 请求该哈希的两个子树的 root
4. 计算机 A 会构建出所需的哈希，并发送给计算机 B
5. 重复步骤 2、3、4，直到发现错误的数据块
这样不需要发送所有的数据便可发现不一致的数据块。
Merkle Tree proofs 可以快速方便地计算出来
Merkle Tree proofs 的数据量较小，可以方便地在全网广播

1.4 比特币中的 Merkle Tree 用例

叶节点存储交易哈希，区块头只需存储 Merkle 根，节省了存储空间。Merkle Tree 可支持 SPV（Simple Payment Verification），在不运行完整区块链网络节点的情况下，也能够对交易数据进行检验。

2023-06-09T09:28:37.png

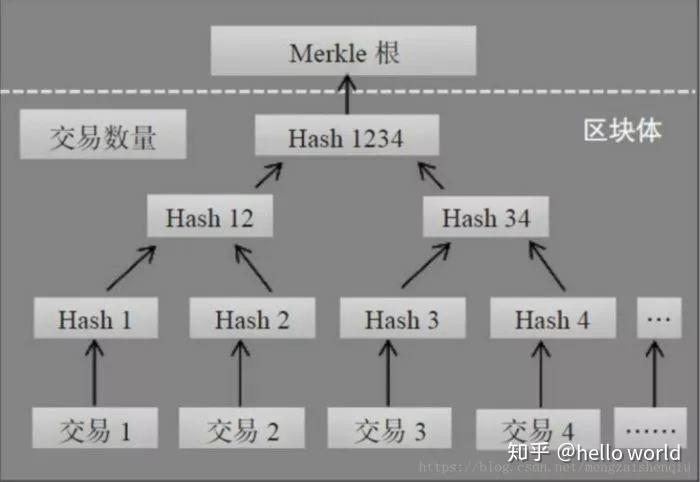
图片来源：https://www.cnblogs.com/bonelee/p/13154709.html

2 Sparse Merkle Tree

Sparse Merkle Tree (SMT) 可以做不存在证明。

SMT 根据 key-value map 构建。每个叶节点都有一个 key 和 value 以及一个哈希属性，该哈希属性是通过将 key 和 value 哈希在一起获得的。叶节点可通过定长 key 来定位。对于给定的数据，树中只有一个位置可以放置该数据。如果该位置为空，则数据不存在。

为此，SMT 大小固定，有 256 级，key 的长度为 256，叶节点数为 2^256。因为 SMT 中大多数数据都不存在，也不需要存储，所以是 Sparse 的。例如，如果子树只有一个非空节点（绿色），可被该非空节点替代。如果子树的节点都为空（白色），可被空节点代替。

2023-06-09T09:28:54.png

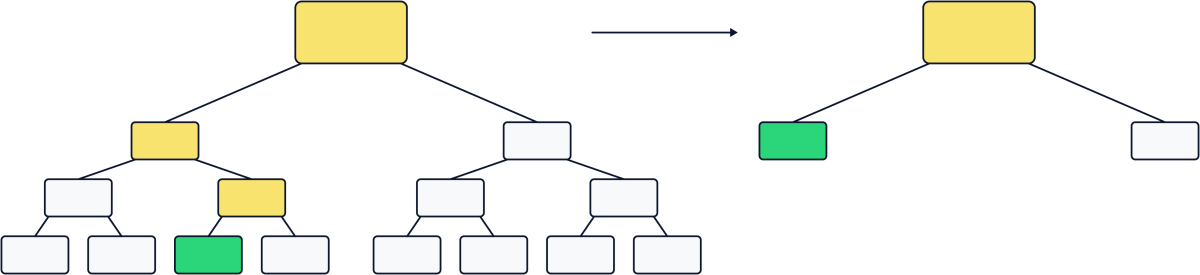
图片来源：https://lisk.com/blog/posts/sparse-merkle-trees-and-new-state-model

SMT 还支持 multiproof，即一次性证明多个节点是否存在，可节省 proof 空间。如下图所示，需要构建节点 A、B、C、D （红色边框）的 multiproof。节点 B、C 存在于树中，而节点 A、D 不存在于树中。multiproof 包含了图中用红色填充的块。

![Untitled](https://s3-us-west-2.amazonaws.com/secure.notion-static.com/8b4951a5-f01c-4aef-9601-2c26a30dc035/Untitled.png)

图片来源：https://lisk.com/blog/posts/sparse-merkle-trees-and-new-state-model

3 代码示例

https://github.com/felicityin/start-smt

4 CKB 中的 SMT 用例

CKB 是一个采用 PoW 共识算法的区块链。

RFC: Compact UDT Lock 中提到了一个例子（应该还没有实现），Tom 将钱 deposit 到 Alice。交易如下所示（只展示 data 部分）：

Inputs:
    <vec> Compact UDT Cell
        Data: <1000 UDT> <old SMT root hash>
    <vec> Tom's UDT Cell
        Data: <2000 UDT>
    <...>
Outputs:
    <vec> Compact UDT Cell
        Data: <1200 UDT> <new SMT root hash>
    <vec> Tom's UDT Cell
        Data: <1799 UDT>
    <...>
Witnesses:
    WitnessArgs structure:
      Lock:
        deposits:
            <vec> Deposit Entry
                source: Tom
                target: Alice
                amount: 200 UDT
                fee: 1 UDT
        transfers: []
        kv_state:
            <vec> Alice's SMT Entry
                k: Alice
                v: 1000 UDT | nonce 5
        kv_proof: <valid proof>
      <...>

该交易结束后，SMT 中会新增如下数据：

Alice’s SMT Entry
    k: Alice
    v: 1200 UDT | nonce 5

合约的验证逻辑：

验证 kv_state 是对的，即 Alice 目前确实是有那么多钱：根据 Witnesses 中的 kv_state 和 kv_proof 计算出 root，与 Inputs 中的 Compact UDT Cell 中的 old SMT root hash 比较，如果一致，则说明 kv_state 是对的。
验证 new SMT root hash 是对的，即 deposit 过程是对的：将 Witnesses 中的 deposits 加到 kv_state，得到新的 kv_state，根据新的 kv_state 和已有的 kv_proof 计算出 root，与 Ouputs 中的 Compact UDT Cell 中的 new SMT root hash 比较，如果一致，则说明 new SMT root hash 是对的。